题目内容
【题目】下面是“作一个
角”的尺规作图过程．
已知：平面内一点A．
求作：
，使得
．
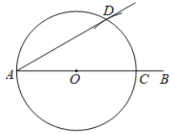
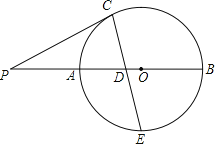
作法：如图，
（1）作射线
；
（2）在射线取一点O，以O为圆心，
为半径作圆，与射线相交于点C；
（3）以C为圆心，
C为半径作弧，与
交于点D，作射线
．
则
即为所求的角．
请回答：该尺规作图的依据是_________________．
【答案】同圆或等圆半径相等，三边相等的三角形是三角形，等边三角形的内角是
，一条弧所对的圆周角是它所对圆心角的一半．
【解析】
根据尺规作图过程，进行证明，即可得出结论．
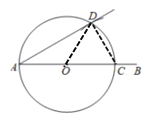
解：证明：连接CD，OD．
由圆的定义和尺规作图得：OD=OC=CD，（圆的半径都相等）
∴△OCD是等边三角形，（三边相等的三角形是三角形）
∴∠DOC=60°，（等边三角形的内角是）
∴
．（一条弧所对的圆周角是它所对圆心角的一半）
故答案为：同圆或等圆半径相等，三边相等的三角形是三角形，等边三角形的内角是，一条弧所对的圆周角是它所对圆心角的一半．
【题目】小腾的爸爸计划将一笔资金用于不超过10天的短期投资，针对这笔资金，银行专属客户经理提供了三种投资方案，这三种方案的回报如下：
方案一：每一天回报30元；
方案二：第一天回报8元，以后每一天比前一天多回报8元；
方案三：第一天回报0.5元，以后每一天的回报是前一天的2倍．
下面是小腾帮助爸爸选择方案的探究过程，请补充完整：
（1）确定不同天数所得回报金额（不足一天按一天计算），如下表：
天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
方案一 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 | 30 |
方案二 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
方案三 | 0.5 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 |
|
其中
________；
（2）计算累计回报金额，设投资天数为
（单位：天），所得累计回报金额是
（单位：元），于是得到三种方案的累计回报金额
，
，
与投资天数的几组对应值：
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 30 | 60 | 90 | 120 | 150 | 180 | 210 | 240 | 270 | 300 |
| 8 | 24 | 48 | 80 | 120 | 168 | 224 | 288 | 360 | 440 |
| 0.5 | 1.5 | 3.5 | 7.5 | 15.5 | 31.5 | 63.5 | 127.5 | 255.5 |
|
其中
________；
（3）在同一平面直角坐标系
中，描出补全后的表中各组数值所对应的点
，
，
，并画出，，的图象；
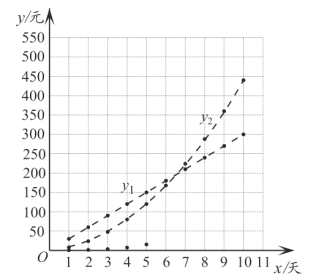
注：为了便于分析，用虚线连接离散的点．
（4）结合图象，小腾给出了依据不同的天数而选择对应方案的建议：
_________________________________________________________________________
