题目内容
(1)找规律:
(m-1)(m+1)=m2-1;
(m-1)(m2+m+1)=m3-1;
(m-1)(m3+m2+m+1)=m4-1;
(m-1)(m4+m3+m2+m+1)=m5-1;
(m-1)(m5+m4+m3+m2+m+1)=______-1;
…
(______)(mn-1+mn-2+…m2+m+1)=______;
在上面空白处填空.
根据你找的规律计算:2+22+23+…+298+299
(2)三角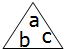 表示3abc,方框
表示3abc,方框 表示-4xywz,求
表示-4xywz,求 ×
× .
.
(m-1)(m+1)=m2-1;
(m-1)(m2+m+1)=m3-1;
(m-1)(m3+m2+m+1)=m4-1;
(m-1)(m4+m3+m2+m+1)=m5-1;
(m-1)(m5+m4+m3+m2+m+1)=______-1;
…
(______)(mn-1+mn-2+…m2+m+1)=______;
在上面空白处填空.
根据你找的规律计算:2+22+23+…+298+299
(2)三角
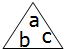 表示3abc,方框
表示3abc,方框 表示-4xywz,求
表示-4xywz,求 ×
× .
.(1)由给出的各等式不难看出以下规律:(m-1)(mn-1+mn-2+…m2+m+1)=mn-1;
令m=2,则(1+2+22+23+…+298+299)(2-1)=2100-1;
故2+22+23+…+298+299=2100-2;
(2)由题意得: 表示3×3mn=9mn;
表示3×3mn=9mn; 表示-4n2m5;
表示-4n2m5;
故 ×
× =9mn×(-4n2m5)=-36m6n3.
=9mn×(-4n2m5)=-36m6n3.
令m=2,则(1+2+22+23+…+298+299)(2-1)=2100-1;
故2+22+23+…+298+299=2100-2;
(2)由题意得:
 表示3×3mn=9mn;
表示3×3mn=9mn; 表示-4n2m5;
表示-4n2m5;故
 ×
× =9mn×(-4n2m5)=-36m6n3.
=9mn×(-4n2m5)=-36m6n3.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目

