题目内容
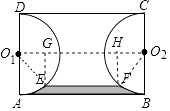
【题目】如图,已知矩形ABCD中,AB=3,AD=2,分别以边AD,BC为直径在矩形ABCD的内部作半圆O1和半圆O2 , 一平行于AB的直线EF与这两个半圆分别交于点E、点F,且EF=2(EF与AB在圆心O1和O2的同侧),则由 ![]() ,EF,
,EF, ![]() ,AB所围成图形(图中阴影部分)的面积等于 .
,AB所围成图形(图中阴影部分)的面积等于 . 
【答案】3﹣ ![]() ﹣
﹣ ![]()
【解析】解:连接O1O2 , O1E,O2F, 则四边形O1O2FE是等腰梯形,
过E作EG⊥O1O2 , 过F⊥O1O2 ,
∴四边形EGHF是矩形,
∴GH=EF=2,
∴O1G= ![]() ,
,
∵O1E=1,
∴GE= ![]() ,
,
∴ ![]() =
= ![]() ;
;
∴∠O1EG=30°,
∴∠AO1E=30°,
同理∠BO2F=30°,
∴阴影部分的面积=S ![]() ﹣2S
﹣2S ![]() ﹣S
﹣S ![]() =3×1﹣2×
=3×1﹣2× ![]() ﹣
﹣ ![]() (2+3)×
(2+3)× ![]() =3﹣
=3﹣ ![]() ﹣
﹣ ![]() .
.
所以答案是:3﹣ ![]() ﹣
﹣ ![]() .
.
【考点精析】本题主要考查了矩形的性质和扇形面积计算公式的相关知识点,需要掌握矩形的四个角都是直角,矩形的对角线相等;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.

练习册系列答案
相关题目
【题目】小明平时喜欢玩“QQ农场”游戏,本学期初二年级数学备课组组织了几次数学反馈性测试,小明的数学成绩如下表:
月份x(月) | 9 | 10 | 11 | 12 | … |
成绩y(分) | 90 | 80 | 70 | 60 | … |
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在下列直角坐标系中描点;

(2)观察①中所描点的位置关系,照这样的发展趋势,猜想y与x之间的函数关系,并求出所猜想的函数表达式;
(3)若小明继续沉溺于“QQ农场”游戏,照这样的发展趋势,请你估计元月份的期末考试中小明的数学成绩,并用一句话对小明提出一些建议.






