题目内容
【题目】如图,△ABC中,CD⊥AB于点D,⊙D经过点B,与BC交于点E,与AB交与点F.已知tanA= ![]() ,cot∠ABC=
,cot∠ABC= ![]() ,AD=8.
,AD=8.
(1)求⊙D的半径;
(2)求CE的长.
【答案】
(1)
【答案】解:∵CD⊥AB,AD=8,tanA= ![]() ,
,
在Rt△ACD中,tanA= ![]() =
= ![]() ,AD=8,CD=4,
,AD=8,CD=4,
在Rt△CBD,cot∠ABC= ![]() =
= ![]() ,BD=3,
,BD=3,
∴⊙D的半径为3
(2)
解:过圆心D作DH⊥BC,垂足为H,
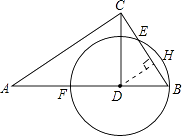
∴BH=EH,
在Rt△CBD中∠CDB=90°,BC= ![]() =5,cos∠ABC=
=5,cos∠ABC= ![]() =
= ![]() ,
,
在Rt△BDH中,∠BHD=90°,cos∠ABC= ![]() =
= ![]() ,BD=3,BH=
,BD=3,BH= ![]() ,
,
∵BH=EH,
∴BE=2BH= ![]() ,
,
∴CE=BC﹣BE=5﹣ ![]() =
= ![]() .
.
【解析】(1)根据三角函数的定义得出CD和BD,从而得出⊙D的半径;
(2)过圆心D作DH⊥BC,根据垂径定理得出BH=EH,由勾股定理得出BC,再由三角函数的定义得出BE,从而得出CE即可.
【考点精析】认真审题,首先需要了解垂径定理(垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目





