题目内容
【题目】抛物线y=ax2+c与x轴交于A、B两点(A在B的左边),与y轴交于点C,抛物线上有一动点P
(1)若A(﹣2,0),C(0,﹣4)
①求抛物线的解析式;
②在①的情况下,若点P在第四象限运动,点D(0,﹣2),以BD、BP为邻边作平行四边形BDQP,求平行四边形BDQP面积的取值范围.
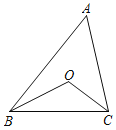
(2)若点P在第一象限运动,且a<0,连接AP、BP分别交y轴于点E、F,则问 ![]() 是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
是否与a,c有关?若有关,用a,c表示该比值;若无关,求出该比值.
【答案】
(1)
解:①∵A(﹣2,0),C(0,﹣4)在抛物线上,
∴ ![]() ,解得
,解得 ![]() ,
,
∴抛物线解析式为y=x2﹣4;
②如图1,连接DB、OP,设P(x,x2﹣4),
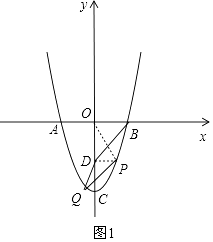
∵A(﹣2,0),对称轴为y轴,
∴B(2,0),
∴S△BDP=S△ODP+S△OBP﹣S△BOD= ![]() OD|x|+
OD|x|+ ![]() OB|x2﹣4|﹣
OB|x2﹣4|﹣ ![]() ODOB=x+4﹣x2﹣2=﹣x2+x+2=﹣(x﹣
ODOB=x+4﹣x2﹣2=﹣x2+x+2=﹣(x﹣ ![]() )2+
)2+ ![]() ,
,
∵点P在第四象限运动,
∴0<x<2,
∴当x= ![]() 时,S△BDP有最大值
时,S△BDP有最大值 ![]() ,当x=2时,S△BDP有最小值0,
,当x=2时,S△BDP有最小值0,
∴0<S△BDP≤ ![]() ,
,
∵四边形BDQC为平行四边形,
∴S四边形BDQP=2S△BDP,
∴0<S四边形BDQP≤ ![]() ;
;
(2)
解:如图2,过点P作PG⊥AB,设A(x1,0),B(x2,0),P(x,y),
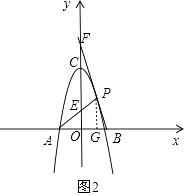
∵PG∥y轴,
∴△AOE∽△AGP,△BGP∽△BOF,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() ,
, ![]() =
= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() +
+ ![]() =
= ![]() =
= ![]() ,
,
当y=0时,可得ax2+c=0,
∴x1+x2=0,x1x2= ![]() ,
,
∴ ![]() +
+ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴OE+OF=2c,
∴ ![]() =
= ![]() =2,
=2,
∴ ![]() =
= 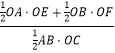 =
= 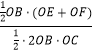 =
= ![]() =1,
=1,
∴ ![]() 的值与a,c无关,比值为1.
的值与a,c无关,比值为1.
【解析】(1)①由A、C两点的坐标,利用待定系数法可求得抛物线解析式;②连接BD、OP,设出P点坐标,利用S△BDP=S△ODP+S△OBP﹣S△BOD可用x表示出四边形BDQP的面积,借助x的取值范围,可求得四边形BDQP面积的取值范围;(2)过点P作PG⊥AB,设A(x1 , 0),B(x2 , 0),P(x,y),由△AOE∽△AGP、△BGP∽△BOF,利用相似三角形的性质和一元二次方程根与系数的关系可整理得到 ![]() =2,再利用三角形的面积可得
=2,再利用三角形的面积可得 ![]() 的值.
的值.
【考点精析】认真审题,首先需要了解相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形).