题目内容
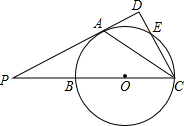 如图,PA切⊙O于A,PBC过圆心O,交⊙O于B、C,CD⊥PA于D,交⊙O于点E.
如图,PA切⊙O于A,PBC过圆心O,交⊙O于B、C,CD⊥PA于D,交⊙O于点E.(1)求证:CA平分∠BCD.
(2)若DC=6,AC=4
| 3 |
(3)作AG⊥BC于G,连接AB、DG,判断AB与DG的位置关系,并证明.
分析:(1)连接OA,由PD为圆的切线,利用切线的性质得到PD与OA垂直,再由CD与PD垂直,确定出OA与CD平行,利用两直线平行得到一对内错角相等,再由OA=OC,利用等边对等角得到一对角相等,等量代换得到一对角相等,即CA为角平分线;
(2)连接AB,由CA为角平分线,得到一对角相等,再由BC为直径,利用直径所对的圆周角为直角得到一对直角相等,利用两对角相等的两三角形相似得到三角形ABC与三角形ACD相似,由相似得比例,将DC与AC的值代入计算即可求出BC的长,进而确定出圆的半径;
(3)AB与DG平行,理由为:过A作AG垂直于BC,连接DG,由CA为角平分线得到一对角相等,再由一对直角相等,AC为公共边,利用AAS得到三角形ACD与三角形ACG全等,利用全等三角形对应边相等得到AD=AG,AC为角平分线,利用三线合一得到AC与DG垂直,再由BA与AC垂直,得到一对直角相等,利用同位角相等两直线平行即可得到AB与DG平行.
(2)连接AB,由CA为角平分线,得到一对角相等,再由BC为直径,利用直径所对的圆周角为直角得到一对直角相等,利用两对角相等的两三角形相似得到三角形ABC与三角形ACD相似,由相似得比例,将DC与AC的值代入计算即可求出BC的长,进而确定出圆的半径;
(3)AB与DG平行,理由为:过A作AG垂直于BC,连接DG,由CA为角平分线得到一对角相等,再由一对直角相等,AC为公共边,利用AAS得到三角形ACD与三角形ACG全等,利用全等三角形对应边相等得到AD=AG,AC为角平分线,利用三线合一得到AC与DG垂直,再由BA与AC垂直,得到一对直角相等,利用同位角相等两直线平行即可得到AB与DG平行.
解答: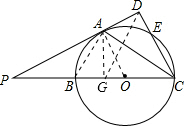 (1)证明:连接OA,
(1)证明:连接OA,
∵PD切⊙O于A,
∴OA⊥PD,
∵CD⊥PD,
∴∠PAO=∠PDC=90°,
∴OA∥CD,
∴∠OAC=∠ACD,
在⊙O中,OA=OC,
∴∠OAC=∠OCA,
∴∠ACD=∠OCA,
∴CA平分∠BCD;
(2)连接BA,
在⊙O中,BC为直径,
∴∠BAC=90°,
∴∠BAC=∠PDC,
∵∠ACO=∠ACD,
∴△BCA∽△ACD,
∴
=
,
∴AC2=BC•DC,即(4
)2=6BC,
∴BC=8,
∴⊙O的半径为4;
(3)AB∥DG,理由为:
证明:∵AG⊥BC,
∴∠AGC=∠ADC=90°,
在△ACG和△ACD中,
,
∴△ACG≌△ACD(AAS),
∴AG=AD,∠GAC=∠DAC,
∴AC⊥GD,
∵BA⊥AC,
∴∠BAC=∠GMC=90°,
∴AB∥DG.
 (1)证明:连接OA,
(1)证明:连接OA,∵PD切⊙O于A,
∴OA⊥PD,
∵CD⊥PD,
∴∠PAO=∠PDC=90°,
∴OA∥CD,
∴∠OAC=∠ACD,
在⊙O中,OA=OC,
∴∠OAC=∠OCA,
∴∠ACD=∠OCA,
∴CA平分∠BCD;
(2)连接BA,
在⊙O中,BC为直径,
∴∠BAC=90°,
∴∠BAC=∠PDC,
∵∠ACO=∠ACD,
∴△BCA∽△ACD,
∴
| AC |
| CD |
| BC |
| AC |
∴AC2=BC•DC,即(4
| 3 |
∴BC=8,
∴⊙O的半径为4;
(3)AB∥DG,理由为:
证明:∵AG⊥BC,
∴∠AGC=∠ADC=90°,
在△ACG和△ACD中,
|
∴△ACG≌△ACD(AAS),
∴AG=AD,∠GAC=∠DAC,
∴AC⊥GD,
∵BA⊥AC,
∴∠BAC=∠GMC=90°,
∴AB∥DG.
点评:此题考查了切线的性质,相似三角形的判定与性质,全等三角形的判定与性质,等腰三角形的性质,平行线的判定与性质,熟练掌握切线的性质是解本题的关键.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
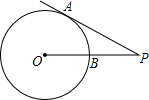 如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为( )
如图,PA切⊙O于点A,PO交⊙O于点B,若PA=6,BP=4,则⊙O的半径为( )A、
| ||
B、
| ||
| C、2 | ||
| D、5 |
 如图,PA切⊙O于点A,PBC是⊙O的割线,且PB=BC,如果PA=3
如图,PA切⊙O于点A,PBC是⊙O的割线,且PB=BC,如果PA=3| 2 |
A、3
| ||
| B、3 | ||
C、
| ||
D、2
|
 如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )
如图,PA切⊙O于点A,PB切⊙O于点B,如果∠APB=60°,⊙O半径是3,则劣弧AB的长为( )A、
| ||
| B、π | ||
| C、2π | ||
| D、4π |
 8、如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径等于( )
8、如图,PA切⊙O于点A,PBC是⊙O的割线且过圆心,PA=4,PB=2,则⊙O的半径等于( ) 如图:PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中错误的是( )
如图:PA切⊙O于A,PB切⊙O于B,OP交⊙O于C,下列结论中错误的是( )