Question

【题目】如图，已知抛物线y＝﹣x2+ax+3的顶点为P，它分别与x轴的负半轴、正半轴交于点A，B，与y轴正半轴交于点C，连接AC，BC，若tan∠OCB﹣tan∠OCA＝．

（1）求a的值；

（2）若过点P的直线l把四边形ABPC分为两部分，它们的面积比为1：2，求该直线的解析式．

Answer 1

【答案】（1）2；（2）y＝﹣8x+12或y＝4x

【解析】

（1）根据抛物线与坐标轴的交点可得一元二次方程，根据韦达定理可得x1+x2＝a；由函数解析式可知当x＝0时y的值，则可得OC的长；结合tan∠OCB﹣tan∠OCA＝得出OB﹣OA＝2，再用x1、x2表示出来，可得a的值；

（2）由（1）可得抛物线的解析式，则可求得点P和点A、点B的坐标，延长PC交x轴于点D，作PF⊥x轴于点F，根据S四边形ABPC＝S△PDB﹣S△CDA，可求得四边形ABPC的面积；设直线l与x轴交于点M（m，0），则BM＝3﹣m，根据直线l把四边形ABPC分为面积比为1：2的两部分，分情况列出关于m的方程，解得m的值，则根据待定系数法可得直线l的解析式．

1）∵抛物线y＝﹣x2+ax+3与x轴交于点A，B，

∴方程﹣x2+ax+3＝0有两个不同的实数根．

设这两个根分别为x1、x2，且x1＜0，x2＞0，

由韦达定理得：x1+x2＝a，

∵当x＝0时，y＝﹣x2+ax+3＝3，

∴OC＝3．

∵tan∠OCB﹣tan∠OCA＝．

∴﹣＝，

∴OB﹣OA＝2，

∴x2﹣（﹣x1）＝2，即x2+x1＝2，

∴a＝2．

（2）由（1）得抛物线的解析式为y＝﹣x2+2x+3，

∴其顶点坐标为P（1，4）．

解方程﹣x2+2x+3＝0，得x1＝﹣1、x2＝3，

∴A（﹣1，0），B（3，0）．

延长PC交x轴于点D，作PF⊥x轴于点F，

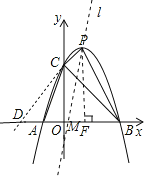
∴S四边形ABPC＝S△PDB﹣S△CDA

＝DBPF﹣DAOC

＝（3+3）×4﹣（3﹣1）×3

＝9．

设直线l与x轴交于点M/span>（m，0），则BM＝3﹣m，

∴S△PMB＝×（3﹣m）×4＝6﹣2m，

当6﹣2m＝×9＝3时，m＝，此时M（，0），

即直线l过点P（1，4），M（，0），

由待定系数法可得l的解析式为y＝﹣8x+12；

同理，当6﹣2m＝×9＝6时，m＝0，此时M（0，0），即直线l过点P（1，4），M（0，0），

由待定系数法可得l的解析式为y＝4x；

综上所述，直线l的解析式为y＝﹣8x+12或y＝4x．