题目内容
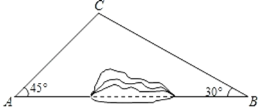
【题目】为缓解交通压力,建设美丽遵义,市政府加快了风新快线的建设.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=8千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
【答案】(1)开通隧道前,汽车从A地到B地要走约13.7千米;(2)开通隧道后,汽车从A地到B地可以少走约2.8千米千米.
【解析】
(1)过点C作AB的垂线CD,垂足为D,先解直角三角形求出CD,再求出AC进而解答即可;
(2)在直角△CBD中,解直角三角形求出BD,再求出AD,进而求出答案.
解:(1)过点C作AB的垂线CD,垂足为D,

∵AB⊥CD,sin30°=![]() ,BC=8千米,
,BC=8千米,
∴CD=BCsin30°=8×![]() =4(千米),
=4(千米),
∴AC=![]() =4
=4![]() (千米),
(千米),
∴AC+BC=8+4![]() ≈13.7(千米),
≈13.7(千米),
答:开通隧道前,汽车从A地到B地要走约13.7千米;
(2)∵cos30°=![]() ,BC=8(千米),
,BC=8(千米),
∴BD=BCcos30°=8×![]() =4
=4![]() (千米),CD=
(千米),CD=![]() BC=4(千米),
BC=4(千米),
∵tan45°=![]() ,
,
∴AD=![]() =4(千米),
=4(千米),
∴AB=AD+BD=4+4![]() ≈10.9(千米),
≈10.9(千米),
∴AC+BC﹣AB=13.7﹣10.9=2.8(千米),
答:开通隧道后,汽车从A地到B地可以少走约2.8千米.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目