题目内容
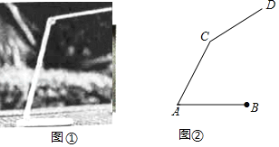
【题目】图①是放置在水平面上的台灯,图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂AC=44cm,灯罩CD=32cm,灯臂与底座构成的∠CAB=60°.CD可以绕点C上下调节一定的角度.使用发现:当CD与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为54.06cm.请通过计算说明此时台灯光线是否为最佳?(参考数据:![]() 取1.73).
取1.73).
【答案】台灯光线为最佳,理由见详解.
【解析】
根据题意可知,本题考察解直角三角形的应用,根据直角三角形的边角关系,运用作辅助线构造直角三角形进行求解.
解:如图,作CE⊥AB于E,DH⊥AB于H,CF⊥DH于F.
∵∠CEH=∠CFH=∠FHE=90°,
∴四边形CEHF是矩形,
∴CE=FH,
在Rt△ACE中,∵AC=44cm,∠A=60°,
∴CE=ACsin60°=38.06cm,
∴FH=CE=38.06cm
∵DH=54.06cm,
∴DF=DH﹣FH=54.06﹣38.06=16cm,
在Rt△CDF中,![]() ,
,
∴∠DCF=30°,∴此时台灯光线为最佳.


练习册系列答案
相关题目