Question

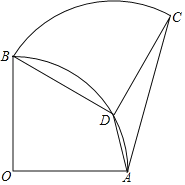
【题目】如图，扇形OAB中，∠AOB＝90°，将扇形OAB绕点B逆时针旋转，得到扇形BDC，若点O刚好落在弧AB上的点D处，则的值为（　　）

A.B.C.D.

Answer 1

【答案】A

【解析】

如图，连OD、AB、BC，延长AD交BC于H点，由旋转的性质可得BD＝BO＝OD＝CD＝OA，∠BDC＝90°，可证△ABC是等边三角形，由线段垂直平分线的性质可得AH垂直平分BC，由等腰直角三角形的性质和等边三角形的性质可得AC＝2CH，AD＝CH-CH，即可求解．

解：如图，连OD、AB、BC，延长AD交BC于H点，

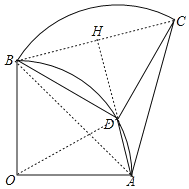
∵将扇形OAB绕点B逆时针旋转，得到扇形BDC，若点O刚好落在弧AB上的点D处，

∴BD＝BO＝OD＝CD＝OA，∠BDC＝90°

∴∠OBD＝60°，即旋转角为60°，

∴∠ABC＝60°，又可知AB＝BC，

∴△ABC是等边三角形，

∵AB＝AC，BD＝CD，

∴AH垂直平分BC，

∴∠CAH＝30°，

∴AC＝2CH，AH＝CH，

∵BD＝CD，∠BDC＝90°，DH⊥BC，

∴DH＝CH，

∴AD＝CH﹣CH，

∴＝．

故选：A．