��Ŀ����
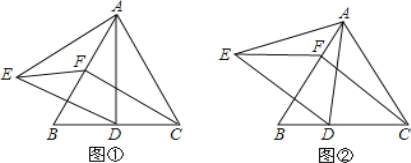
����Ŀ����ͼ���ڰ뾶Ϊ2������AOB�У���AOB��90������C�ǻ�AB�ϵ�һ������(�����A��B�غ�)��OD��BC��OE��AC������ֱ�ΪD��E.

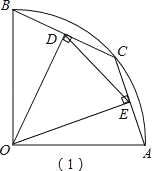
(1)��BC��1ʱ�����߶�OD�ij���
(2)�ڡ�DOE���Ƿ���ڳ��ȱ��ֲ���ıߣ�������ڣ���ָ�������䳤�ȣ���������ڣ���˵�����ɣ�
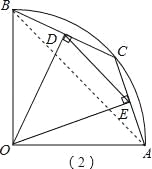
(3)��BD��x����DOE�����Ϊy����y����x�ĺ�������ʽ����д���Ա�����ȡֵ��Χ��
���𰸡���1��OD=![]() ��2��DE=
��2��DE=![]() �����Ȳ��䣨3��y=
�����Ȳ��䣨3��y=![]() ��0��x��
��0��x��![]() ��
��
�������������������1������OD��BC�ɵó�BD=![]() BC=
BC=![]() ����Rt��BOD�����ù��ɶ����������OD�ij���
����Rt��BOD�����ù��ɶ����������OD�ij���
��2������AB������AOB�ǵ���ֱ�������οɵó�AB�ij����ٸ���D��E���е�ɵó�DE=![]() ��
��
��3����BD=x����֪OD=![]() ��������1=��2����3=��4��������2+��3=45������D��DF��OE��DF=
��������1=��2����3=��4��������2+��3=45������D��DF��OE��DF=![]() ��EF=
��EF=![]() x���ɵó����ۣ�
x���ɵó����ۣ�
�����������1����ͼ��1������OD��BC����BD=![]() BC=
BC=![]() ����OD=
����OD=![]() =
=![]() ��
��
��2����ͼ��2�������ڣ�DE�Dz���ģ�
����AB����AB=![]() =2
=2![]() ��
��
��D��E�ֱ����߶�BC��AC���е㣬
��DE=![]() AB=
AB=![]() ��
��
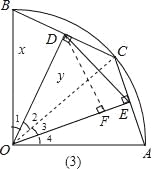
��3����ͼ��3��������OC��
��BD=x��
��OD=![]() ��
��
�ߡ�1=��2����3=��4��
���2+��3=45����
��D��DF��OE��
��DF=![]() =
=![]() ���ɣ�2����֪DE=
���ɣ�2����֪DE=![]() ��
��
����Rt��DEF��EF=![]() =
=![]() ��
��
��OE=OF+EF=![]() +
+![]() =
=![]()
��y=![]() DFOE=
DFOE=![]()
![]()
=![]() ��0��x��
��0��x��![]() ����
����

 ���ݼ���ϵ�д�
���ݼ���ϵ�д�����Ŀ��ijУΪ���˽�ѧ�������Ķ��������������50��ѧ����ͳ������ƽ��ÿ������Ķ�ʱ�䣨tСʱ��������t�ij��̷�ΪA��B��C��D���࣬�����Ǹ����������������Ƶ�������������ͳ��ͼ���������ͼ���ṩ����Ϣ�������������⣺
��1��������е�a��ֵ������ͼ�в�ȫ����ͳ��ͼ��
��2����У����1300��ѧ����������Ƹ�У���ж�����ѧ�������Ķ�ʱ�䲻����1Сʱ��50��ѧ��ƽ��ÿ������Ķ�ʱ��ͳ�Ʊ�
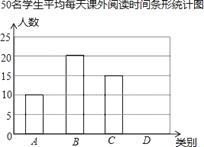
��� | ʱ��t��Сʱ�� | ���� |
A | t��0.5 | 10 |
B | 0.5��t��1 | 20 |
C | 1��t��1.5 | 15 |
D | t��1.5 | a |