题目内容
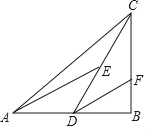
【题目】如图,△ABC是等边三角形,点D是边BC上的一点,以AD为边作等边△ADE,过点C作CF∥DE交AB于点F.
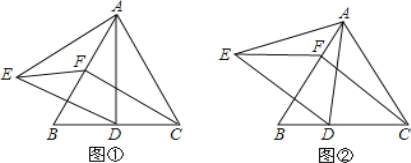
(1)若点D是BC边的中点(如图①),求证:EF=CD;
(2)在(1)的条件下直接写出△AEF和△ABC的面积比;
(3)若点D是BC边上的任意一点(除B、C外如图②),那么(1)中的结论是否仍然成立?若成立,给出证明;若不成立,说明理由.
【答案】(1)证明见解析(2)1:4(3)成立.
【解析】(1)∵△ABC是等边三角形,D是BC的中点,
∴AD⊥BC,且∠BAD=![]() ∠BAC=30°,
∠BAC=30°,
∵△AED是等边三角形,
∴AD=AE,∠ADE=60°,
∴∠EDB=90°-∠ADE=90°-60°=30°,
∵ED∥CF,
∴∠FCB=∠EDB=30°,
∵∠ACB=60°,
∴∠ACF=∠ACB-∠FCB=30°,
∴∠ACF=∠BAD=30°,
在△ABD和△CAF中,
 ,
,
∴△ABD≌△CAF(ASA),
∴AD=CF,
∵AD=ED,
∴ED=CF,
又∵ED∥CF,
∴四边形EDCF是平行四边形,
∴EF=CD.
(2)△AEF和△ABC的面积比为:1:4
(3)成立.
理由如下:∵ED∥FC,
∴∠EDB=∠FCB,
∵∠AFC=∠B+∠BCF=60°+∠BCF,∠BDA=∠ADE+∠EDB=60°+∠EDB
∴∠AFC=∠BDA,
在△ABD和△CAF中,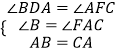
∴△ABD≌△CAF(AAS),
∴AD=FC,
∵AD=ED,
∴ED=CF,
又∵ED∥CF,
∴四边形EDCF是平行四边形,
∴EF=DC.

【题目】某校为了解学生最喜欢的球类运动情况,随机选取该校部分学生进行调查,要求每名学生只写一类最喜欢的球类运动,以下是根据调查结果绘制的统计图的一部分,
类别 |
|
|
|
|
|
|
类型 | 足球 | 羽毛球 | 乒乓球 | 篮球 | 排球 | 其它 |
人数 |
|
|
|
|

根据以上信息,解答下列问题:
(1)被调查学生的总人数为 人.
(2)最喜欢篮球的有 人,最喜欢足球的学生数占被调查总人数的百分比为 %
(3)该校共有![]() 名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?
名学生,根据调查结果,估计该校最喜欢排球的学生人数有多少?