题目内容
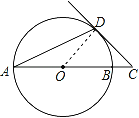
【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°.
(1)求证:CD是⊙O的切线.
(2)若AB=2![]() ,求OC的长.
,求OC的长.

【答案】(1)、证明过程见解析;(2)、2.
【解析】
试题分析:(1)、连接DO,由三角形的外角与内角的关系易得∠DOC=∠C=45°,故有∠ODC=90°,即CD是圆的切线.(2)、由1知,CD=OD=![]() AB,在直角△COD中,利用勾股定理即可求解.
AB,在直角△COD中,利用勾股定理即可求解.
试题解析:(1)、连接DO, ∵AO=DO, ∴∠DAO=∠ADO=22.5°. ∴∠DOC=45°.
又∵∠ACD=2∠DAB, ∴∠ACD=∠DOC=45°. ∴∠ODC=90°. 又∵OD是⊙O的半径,
∴CD是⊙O的切线.
(2)、连接DB, ∵直径AB=2![]() ,△OCD为等腰直角三角形, ∴CD=OD=
,△OCD为等腰直角三角形, ∴CD=OD=![]() ,OC=2.
,OC=2.

练习册系列答案
相关题目