题目内容
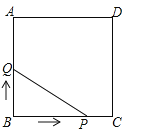
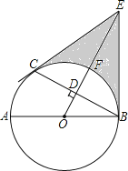
【题目】如图,已知∠AOB=90°,∠OAB=30°,反比例函数![]() 的图象过点
的图象过点![]() ,反比例函数
,反比例函数![]() 的图象过点A
的图象过点A
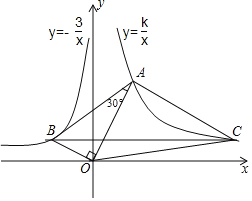
(1)求![]() 和
和![]() 的值.
的值.
(2)过点B作BC∥x轴,与双曲线![]() 交于点C,求△OAC的面积.
交于点C,求△OAC的面积.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)把点B![]() 代入
代入![]() 可求出a值,进而可求出OE、BE的长,分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,可证明△BOE∽△OAD,根据相似三角形的性质及正切的定义可得
可求出a值,进而可求出OE、BE的长,分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,可证明△BOE∽△OAD,根据相似三角形的性质及正切的定义可得![]() ,即可求出AD和OD的长,可得A点坐标,代入
,即可求出AD和OD的长,可得A点坐标,代入![]() 即可求出k值;(2)过点C作CF⊥x轴于F,由B点坐标可知C点纵坐标,由C点在
即可求出k值;(2)过点C作CF⊥x轴于F,由B点坐标可知C点纵坐标,由C点在![]() 图象上,可求出C点横坐标,可得CF的长,由点A、点C在反比例函数
图象上,可求出C点横坐标,可得CF的长,由点A、点C在反比例函数![]() 图象上,可得S△AOD=S△COF,根据
图象上,可得S△AOD=S△COF,根据![]()
![]() 即可得答案.
即可得答案.
(1)∵反比例函数![]() 经过点B
经过点B![]()
∴![]()
∴OE=3,BE=1,
如图,分别过点A、B作AD⊥x轴于D,BE⊥x轴于E,
∵∠AOB=90°,
∴∠EOB+∠AOD=90°,
∵∠AOD+∠OAD=90°,
∴∠EOB=∠OAD,
又∵∠BEO=∠ODA=90°,
∴△BOE∽△OAD,
∴![]() ,
,
∴AD=![]() OE=3
OE=3![]() ,OD=
,OD=![]() BE=
BE=![]() ,
,
∴![]() ,
,
∴![]() .
.
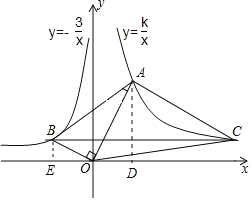
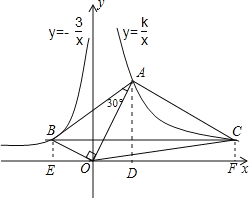
(2)如图,过点C作CF⊥x轴于F
由(1)可知AD=![]() ,OD=
,OD=![]() ,
,
∵BC∥x轴,B(-3,1),
∴![]() =1,
=1,
∵点C在双曲线![]() 上,
上,
∴![]() =9,
=9,
∴C(9,1),
∴CF=1,
∵点A、点C在反比例函数![]() 图象上,
图象上,
∴S△AOD=S△COF,
∴![]()
![]() ,
,
∴![]()
![]()
![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目