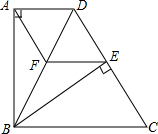
题目内容
在△ABC中，AB=AC，∠BAC=120°，过点C作CD∥AB，且CD=2AB，连接BD，BD=2．求△ABC的面积．
过点B作BE∥AC交CD于E，过B作BF⊥CD于F，
∵CD∥AB，AB=AC，
∴四边形ABEC是菱形，
∴BE=CE=AB，
∵∠BAC=120°，
∴∠ABE=60°，
∴∠BED=∠ABE=60°，
∵CD=2AB，BD=2，
∴CE=DE=BD=2，
∴△BDE是等边三角形，
∴△BDE的高BF=
=
，
∴S△ABC=
S菱形ABEC=
×2×
=
，
故△ABC的面积为
．
∵CD∥AB，AB=AC，
∴四边形ABEC是菱形，
∴BE=CE=AB，
∵∠BAC=120°，
∴∠ABE=60°，
∴∠BED=∠ABE=60°，
∵CD=2AB，BD=2，
∴CE=DE=BD=2，
∴△BDE是等边三角形，
∴△BDE的高BF=
| 22-12 |
| 3 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故△ABC的面积为
| 3 |
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
