题目内容
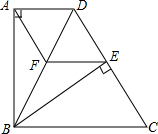
如图，四边形ABCD中，AD∥BC，BA⊥AD，BC=DC，BE⊥CD于点E．
（1）求证：△ABD≌△EBD；
（2）过点E作EF∥DA，交BD于点F，连接AF．求证：四边形AFED是菱形．
（1）求证：△ABD≌△EBD；
（2）过点E作EF∥DA，交BD于点F，连接AF．求证：四边形AFED是菱形．
证明：（1）如图，
∵AD∥BC，
∴∠1=∠DBC．
∵BC=DC，
∴∠2=∠DBC．
∴∠1=∠2．
∵BA⊥AD，BE⊥CD
∴∠BAD=∠BED=90°，
在△ABD和△EBD中
，
∴△ABD≌△EBD（AAS）；
（2）由（1）得，AD=ED，∠1=∠2．
∵EF∥DA，
∴∠1=∠3．
∴∠2=∠3．
∴EF=ED．
∴EF=AD．
∴四边形AFED是平行四边形．
又∵AD=ED，
∴四边形AFED是菱形．
∵AD∥BC，
∴∠1=∠DBC．
∵BC=DC，
∴∠2=∠DBC．
∴∠1=∠2．
∵BA⊥AD，BE⊥CD
∴∠BAD=∠BED=90°，
在△ABD和△EBD中
|
∴△ABD≌△EBD（AAS）；
（2）由（1）得，AD=ED，∠1=∠2．
∵EF∥DA，
∴∠1=∠3．
∴∠2=∠3．
∴EF=ED．
∴EF=AD．
∴四边形AFED是平行四边形．
又∵AD=ED，
∴四边形AFED是菱形．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
