题目内容
如图,已知在四边形ABFC中∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE.
(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)若四边形BECF的面积是6cm2且BC+AC=
cm时.求AB.

(1)试探究,四边形BECF是什么特殊的四边形并证明之;
(2)若四边形BECF的面积是6cm2且BC+AC=
| 105 |

(1)四边形BECF是菱形.
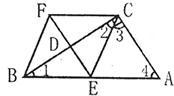 证明:EF垂直平分BC,
证明:EF垂直平分BC,
∴BF=FC,BE=EC,
∴∠1=∠2,
∵∠ACB=90°,
∴∠1+∠4=90°,∠3+∠2=90°,
∴∠3=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)由(1)可知四边形AEFC为平行四边形,
∴EF=AC,
根据菱形的面积公式可知:BC•AC=6×2=12(cm)2,
又BC+AC=
cm,
∴(BC+AC)2-2BC•AC=BC2+AC2=105-2×12=81(cm)2,
∴AB=2BE=2×
=9cm.
 证明:EF垂直平分BC,
证明:EF垂直平分BC,∴BF=FC,BE=EC,
∴∠1=∠2,
∵∠ACB=90°,
∴∠1+∠4=90°,∠3+∠2=90°,
∴∠3=∠4,
∴EC=AE,
∴BE=AE,
∵CF=AE,
∴BE=EC=CF=BF,
∴四边形BECF是菱形.
(2)由(1)可知四边形AEFC为平行四边形,
∴EF=AC,
根据菱形的面积公式可知:BC•AC=6×2=12(cm)2,
又BC+AC=
| 105 |
∴(BC+AC)2-2BC•AC=BC2+AC2=105-2×12=81(cm)2,
∴AB=2BE=2×
|

练习册系列答案
相关题目



 面积.
面积.