题目内容
【题目】某公司在A，B两地分别有同型号的机器17台和15台，目前需要把这些机器中的18台运往甲地，14台运往乙地．从A，B两地运往甲，乙两地的费用如表：
甲地（元/台） | 乙地（元/台） | |
A地 | 600 | 500 |
B地 | 400 | 800 |
（1）设从A地运往甲地x台，则从A地运往乙地 台，从B地运往乙地 台．（结果用x的代数式表示，且代数式化到最简）
（2）当运送总费用为15800元时，请确定运送方案（即A，B两地运往甲、乙两地的机器各几台）．
（3）能否有一种运送方案比（2）中方案的总运费低？如果有，直接写出运送方案及所需运费；如果没有，请说明理由．
【答案】（1）17﹣x，x﹣3；（2）当运送总费用为15800元时，从A地运往甲地5台，运往乙地12台；从B地运往甲地13台，运往乙地2台；（3）从A地运往甲地3台，运往乙地14台；从B地运往甲地15台，运往乙地0台．最低运费为14800元．
【解析】
（1）按题目的数量关系计算即可得答案．
（2）把每种情况的运费与相应的数量相乘，再把积相加，即为总运费，列得方程并求解．
（3）设总运费为y，可列得y关于x的函数关系式，再根据一次函数性质和x的取值范围，即能求得运费最小值．
解：（1）∵A地有17台机器，运往甲地x台
∴剩（17﹣x）台运往乙地
∵需运14台机器到乙地，A地已运（17﹣x）台过来
∴剩下需由B地运来的台数为：14﹣（17﹣x）＝x﹣3
故答案为：17﹣x；x﹣3
（2）依题意得：600x+500（17﹣x）+400（18﹣x）+800（x﹣3）＝15800
解得：x＝5
∴17﹣x＝12，18﹣x＝13，x﹣3＝2
答：当运送总费用为15800元时，从A地运往甲地5台，运往乙地12台；从B地运往甲地13台，运往乙地2台．
（3）有运送方案比（2）中方案的总运费低．
设总运费为y元，得：
y＝600x+500（17﹣x）+400（18﹣x）+800（x﹣3）＝500x+13300
y随x增大而增大
又∵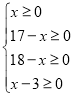
得：3≤x≤17
∴当x＝3时，y有最小值，为y＝500×3+13300＝14800
∴方案为：从A地运往甲地3台，运往乙地14台；从B地运往甲地15台，运往乙地0台．最低运费为14800元．
