题目内容
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”就是一例.如图,这个三角形的构造法则:两腰上的数都是1,其余每个数均为其上方左右两数之和,它给出了(a+b)n(n为正整数)的展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应(a+b)2=a2+2ab+b2展开式中的系数;第四行的四个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中的系数等等.
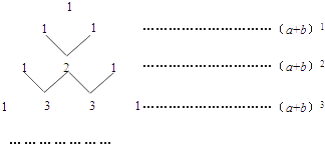
(1)根据上面的规律,则(a+b)5的展开式=________.
(2)利用上面的规律计算:25﹣5×24+10×23﹣10×22+5×2﹣1=________.
【答案】(1)(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;(2)1.
【解析】
(1)根据规律得出(a+b)1,(a+b)2,(a+b)3,(a+b)4的值,即可推出
(a+b)5的值;
(2)根据规律得出原式=(2﹣1)5 ,求出即可.
(1.)∵(a+b)1=a+b, (a+b)2=a2+2ab+b2 ,
(a+b)3=a3+3a2b+3ab2+b3 ,
(a+b)4=a4+4a3b+6a2b2+4ab3+b4 ,
∴(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5 ,
故答案为:(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5;
(2.)25﹣5×24+10×23﹣10×22+5×2﹣1=(2﹣1)5=15=1(根据(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5的逆运用得出的),
故答案为:1.

【题目】某公司在A,B两地分别有同型号的机器17台和15台,目前需要把这些机器中的18台运往甲地,14台运往乙地.从A,B两地运往甲,乙两地的费用如表:
甲地(元/台) | 乙地(元/台) | |
A地 | 600 | 500 |
B地 | 400 | 800 |
(1)设从A地运往甲地x台,则从A地运往乙地 台,从B地运往乙地 台.(结果用x的代数式表示,且代数式化到最简)
(2)当运送总费用为15800元时,请确定运送方案(即A,B两地运往甲、乙两地的机器各几台).
(3)能否有一种运送方案比(2)中方案的总运费低?如果有,直接写出运送方案及所需运费;如果没有,请说明理由.