题目内容
【题目】将连续的奇数1，3，5，7，9，…，排列成如图所示的数表：
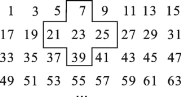
（1）十字框中的五个数的和与中间数23有什么关系？
（2）设中间数为
，用式子表示十字框中五个数之和.
（3）将十字框上、下、左、右平移，可框住另外五个数，这五个数还有这种规律吗？
（4）十字框中的五个数之和能等于2015吗？若能，请写出这五个数；若不能，请说明理由.
【答案】（1）十字框中的五个数的和是中间数23的5倍；（2）
；（3）这五个数仍具有这种规律；（4）十字框中的五个数之和能等于2015.这五个数分别为387，401，403，405，419.
【解析】
（1）计算十字框中五个数的和即可得到与23的关系；
（2）由（1）计算的规律可以直接写出结果；
（3）由（1）（2）可以直接得出一般性的结论；
（4）根据上面的规律，有5a＝2015，据此求得a的值．
解：（1）计算十字框中五个数的和，
得
，而
，
所以十字框中的五个数的和是中间数23的5倍.
（2）若中间数为
，则十字框中五个数之和用式子表示是.
（3）通过计算，不管框住怎样的五个数，这五个数仍具有这种规律.
（4）若能等于2015，根据上面的规律，有
，解得
.因为403是奇数，所以十字框中的五个数之和能等于2015.这五个数分别为387，401，403，405，419.
优加精卷系列答案
【题目】某公司在A，B两地分别有同型号的机器17台和15台，目前需要把这些机器中的18台运往甲地，14台运往乙地．从A，B两地运往甲，乙两地的费用如表：
甲地（元/台） | 乙地（元/台） | |
A地 | 600 | 500 |
B地 | 400 | 800 |
（1）设从A地运往甲地x台，则从A地运往乙地 台，从B地运往乙地 台．（结果用x的代数式表示，且代数式化到最简）
（2）当运送总费用为15800元时，请确定运送方案（即A，B两地运往甲、乙两地的机器各几台）．
（3）能否有一种运送方案比（2）中方案的总运费低？如果有，直接写出运送方案及所需运费；如果没有，请说明理由．
【题目】某食品厂从生产的袋装食品中抽出样品20袋，检测每袋的质量是否符合标准，超过或不足的部分分别用正、负数来表示，记录如下表：
与标准质量的差值 （单位：克） |
|
| 0 | 1 | 3 | 6 |
袋 数 | 1 | 4 | 3 | 4 | 5 | 3 |
（1）这批样品的平均质量比标准质量多还是少？多或少几克？
（2）若标准质量为450克，则抽样检测的20袋食品的总质量为多少克？
（3）若该种食品的合格标准为450±5克，求该食品的抽样检测的合格率．
【题目】2013年安庆市体育考试跳绳项目为学生选考项目，下表是某班模拟考试时10名同学的测试成绩（单位：个/分钟），则关于这10名同学每分钟跳绳的测试成绩，下列说法错误的是（ ）
成绩（个/分钟） | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
A. 众数是177 B. 平均数是170 C. 中位数是173.5 D. 方差是135
