题目内容
【题目】如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在线段OA,OC上,且OB=OD,∠1=∠2,AE=CF.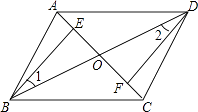
(1)证明:△BEO≌△DFO;
(2)证明:四边形ABCD是平行四边形.
【答案】
(1)证明:∵∠EOB与∠FOD是对顶角,
∴∠EOB=∠FOD,
在△BEO和△DFO中 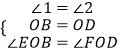
∴△BEO≌△DFO(ASA)
(2)证明:由(1)可知△BEO≌△DFO,
∴OE=OF,
∵AE=CF,
∴OA=OC,
∵OB=OD,
∴四边形ABCD为平行四边形.
【解析】(1)利用ASA易证出△BEO≌△DFO;
(2)由(1)中△BEO≌△DFO可得OE=OF。进而可得OA=OC,利用对角线互相平分的四边形是平行四边形可以证出结论.
【考点精析】本题主要考查了平行四边形的判定的相关知识点,需要掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形才能正确解答此题.

 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案【题目】5.1劳动节,某校决定组织甲乙两队参加义务劳动,并购买队服.下面是服装厂给出的服装的价格表:
购买服装的套数 |
|
|
|
每套服装的价格 |
|
|
|
经调查:两个队共75人(甲队人数不少于40人),如果分别各自购买队服,两队共需花费5600元,请回答以下问题:
(1)如果甲、乙两队联合起来购买服装,那么比各自购买服装最多可以节省_________.
(2)甲、乙两队各有多少名学生?
(3)到了现场,因工作分配需要,临时决定从甲队抽调a人,从乙队抽调b人,组成丙队(要求从每队抽调的人数不少于10人),现已知重新组队后,甲队平均每人需植树1棵;乙队平均每人需植树4棵;丙队平均每人需植树6棵,甲乙丙三队共需植树265棵,请写出所有的抽调方案.