Question

【题目】将边长为2的正方形OABC如图放置，O为原点．若∠α=15°，则点B的坐标为 ．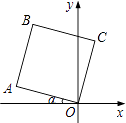

Answer 1

【答案】（﹣ , ）
【解析】解：连接OB，过B作BE⊥x轴于E，则∠BEO=90°，

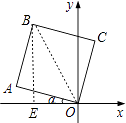
∵四边形OABC是正方形，

∴AB=OA=2，∠A=90°，∠BOA=45°，

由勾股定理得：OB= =2 ，

∵∠α=15°，∠BOA=45°，

∴∠BOE=45°+15°=60°，

在Rt△BOE中，BE=OB×sin60°=2 × = ，OE=OB×cos60°= ，

∴B的坐标为（﹣ ， ）．

所以答案是：

【考点精析】通过灵活运用勾股定理的概念和正方形的性质，掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形即可以解答此题．