题目内容
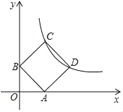
【题目】如图,在平面直角坐标系中放置一直角三角板,其顶点为![]() ,
,![]() ,
,![]() ,将此三角板绕原点
,将此三角板绕原点![]() 顺时针旋转
顺时针旋转![]() ,得到
,得到![]() .
.
(1)如图,一抛物线经过点![]() ,求该抛物线解析式;
,求该抛物线解析式;
(2)设点![]() 是在第一象限内抛物线上一动点,求使四边形
是在第一象限内抛物线上一动点,求使四边形![]() 的面积达到最大时点
的面积达到最大时点![]() 的坐标及面积的最大值.
的坐标及面积的最大值.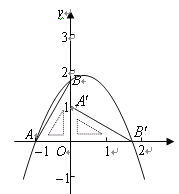
【答案】解:(1)∵抛物线过![]()
设抛物线的解析式为![]()
又∵抛物线过![]() ,将坐标代入上解析式得:
,将坐标代入上解析式得:
![]()
![]()
即满足条件的抛物线解析式为![]()
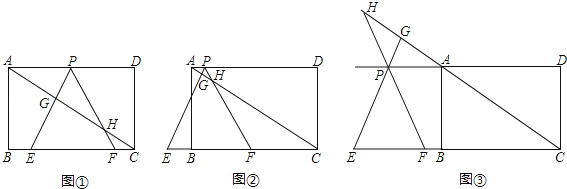
(2)(解法一):如图1,∵![]() 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
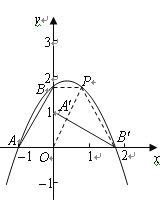
设![]() 则
则![]()
![]() 点坐标满足
点坐标满足![]()
连接![]()
![]()
![]()
=![]()
当![]() 时,
时,![]() 最大.
最大.
此时,![]() .即当动点
.即当动点![]() 的坐标为
的坐标为![]() 时,
时,
![]() 最大,最大面积为
最大,最大面积为![]()
(解法二):如图2,连接![]()
![]() 为第一象限内抛物线上一动点,
为第一象限内抛物线上一动点,
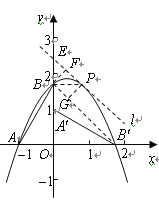
![]() 且
且![]() 的面积为定值,
的面积为定值,
![]() 最大时
最大时![]() 必须最大.
必须最大.
∵![]() 长度为定值,∴
长度为定值,∴![]() 最大时点
最大时点![]() 到
到![]() 的距离最大.
的距离最大.
即将直线![]() 向上平移到与抛物线有唯一交点时,
向上平移到与抛物线有唯一交点时,
![]() 到
到![]() 的距离最大.
的距离最大.
设与直线![]() 平行的直线
平行的直线![]() 的解析式为
的解析式为![]()
联立![]()
得![]()
令![]()
解得![]() 此时直线
此时直线![]() 的解析式为:
的解析式为:![]()
 解得
解得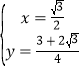
∴直线![]() 与抛物线唯一交点坐标为
与抛物线唯一交点坐标为![]()
设![]() 与
与![]() 轴交于
轴交于![]() 则
则![]()
过![]() 作
作![]() 于
于![]() 在
在![]() 中,
中,![]()
过![]() 作
作![]() 于
于![]() 则
则![]() 到
到![]() 的距离
的距离![]()
此时四边形![]() 的面积最大.
的面积最大.
∴![]() 的最大值=
的最大值=![]()
![]()
【解析】
(1)由![]() 三点的坐标根据待定系数法即可求出解析式;
三点的坐标根据待定系数法即可求出解析式;
(2)先根据题意列出函数关系式,再根据函数关系式的特征即可得到最大值。

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目