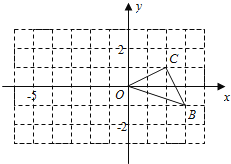
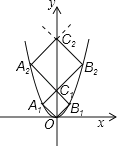
ЬтФПФкШн
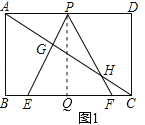
ЁОЬтФПЁПШчЭМЂйЃЌдкОиаЮABCDжаЃЌABЃН![]() ЃЌBCЃН3ЃЌдкBCБпЩЯШЁСНЕуEЁЂFЃЈЕуEдкЕуFЕФзѓБпЃЉЃЌвдEFЮЊБпЫљзїЕШБпЁїPEFЃЌЖЅЕуPЧЁКУдкADЩЯЃЌжБЯпPEЁЂPFЗжБ№НЛжБЯпACгкЕуGЁЂHЃЎ
ЃЌBCЃН3ЃЌдкBCБпЩЯШЁСНЕуEЁЂFЃЈЕуEдкЕуFЕФзѓБпЃЉЃЌвдEFЮЊБпЫљзїЕШБпЁїPEFЃЌЖЅЕуPЧЁКУдкADЩЯЃЌжБЯпPEЁЂPFЗжБ№НЛжБЯпACгкЕуGЁЂHЃЎ
ЃЈ1ЃЉЧѓЁїPEFЕФБпГЄЃЛ
ЃЈ2ЃЉШєЁїPEFЕФБпEFдкЯпЖЮCBЩЯвЦЖЏЃЌЪдВТЯыЃКPHгыBEгаКЮЪ§СПЙиЯЕЃПВЂжЄУїФуВТЯыЕФНсТлЃЛ
ЃЈ3ЃЉШєЁїPEFЕФБпEFдкЩфЯпCBЩЯвЦЖЏЃЈЗжБ№ШчЭМЂкКЭЭМЂлЫљЪОЃЌCFЃО1ЃЌPВЛгыAжиКЯЃЉЃЌЃЈ2ЃЉжаЕФНсТлЛЙГЩСЂТ№ЃПШєВЛГЩСЂЃЌжБНгаДГіФуЗЂЯжЕФаТНсТлЃЎ
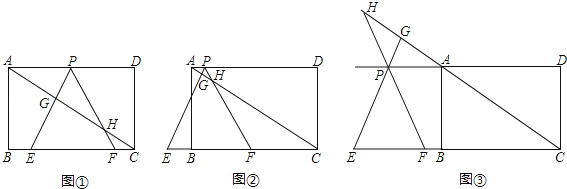
ЁОД№АИЁПЃЈ1ЃЉЁїPEFЕФБпГЄЮЊ2ЃЛЃЈ2ЃЉPHЉBE=1ЃЌжЄУїЙ§ГЬМћНтЮіЃЛЃЈ3ЃЉНсТлВЛГЩСЂЃЌЕБ1ЃМCFЃМ2ЪБЃЌPH=1ЉBEЃЌЕБ2ЃМCFЃМ3ЪБЃЌPH=BEЉ1ЃЎ
ЁОНтЮіЁП
ЪдЬтЙ§PзїPQЁЭBCЃЌДЙзуЮЊQЃЌгЩЫФБпаЮABCDЮЊОиаЮЃЌЕУЕНЁЯBЮЊжБНЧЃЌЧвADЁЮBCЃЌЕУЕНPQ=ABЃЌгжЁїPEFЮЊЕШБпШ§НЧаЮЃЌИљОнЁАШ§ЯпКЯвЛЁБЕУЕНЁЯFPQЮЊ30ЁуЃЌдкRtЁїPQFжаЃЌЩшГіQFЮЊxЃЌдђPF=2xЃЌгЩPQЕФГЄЃЌИљОнЙДЙЩЖЈРэСаГіЙигкxЕФЗНГЬЃЌЧѓГіxЕФжЕЃЌМДПЩЕУЕНPFЕФГЄЃЌМДЮЊЕШБпШ§НЧаЮЕФБпГЄЃЛ
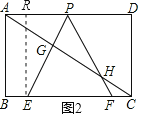
PHЉBE=1ЃЌЙ§EзїERДЙжБгкADЃЌШчЭМЫљЪОЃЌЪзЯШжЄУїЁїAPHЮЊЕШбќШ§НЧаЮЃЌдкИљОнОиаЮЕФЖдБпЦНааЕУЕНвЛЖдФкДэНЧЯрЕШЃЌПЩЕУЁЯAPE=60ЁуЃЌдкRtЁїPERжаЃЌЁЯREP=30ЁуЃЌИљОнжБНЧШ§НЧаЮжаЃЌ30ЁуНЧЫљЖдЕФжБНЧБпЕШгкаББпЕФвЛАыЃЌгЩPEЧѓГіPRЃЌгЩPA=PHЃЌдђPHЉBE=PAЉBE=PAЉAR=PRЃЌМДПЩЕУЕНСНЯпЖЮЕФЙиЯЕЃЛ
ЕБШєЁїPEFЕФБпEFдкЩфЯпCBЩЯвЦЖЏЪБЃЈ2ЃЉжаЕФНсТлВЛГЩСЂЃЌгЩЃЈ2ЃЉЕФНтЬтЫМТЗПЩжЊЕБ1ЃМCFЃМ2ЪБЃЌPH=1ЉBEЃЌЕБ2ЃМCFЃМ3ЪБЃЌPH=BEЉ1ЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉЙ§PзїPQЁЭBCгкQЃЈШчЭМ1ЃЉЃЌ ЁпЫФБпаЮABCDЪЧОиаЮЃЌ ЁрЁЯB=90ЁуЃЌМДABЁЭBCЃЌ
гжЁпADЁЮBCЃЌ ЁрPQ=AB=![]() ЃЌ ЁпЁїPEFЪЧЕШБпШ§НЧаЮЃЌ ЁрЁЯPFQ=60ЁуЃЌ
ЃЌ ЁпЁїPEFЪЧЕШБпШ§НЧаЮЃЌ ЁрЁЯPFQ=60ЁуЃЌ
дкRtЁїPQFжаЃЌЁЯFPQ=30ЁуЃЌ ЩшPF=2xЃЌQF=xЃЌPQ=![]() ЃЌИљОнЙДЙЩЖЈРэЕУЃК
ЃЌИљОнЙДЙЩЖЈРэЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃКx=1ЃЌЙЪPF=2ЃЌ ЁрЁїPEFЕФБпГЄЮЊ2ЃЛ
ЃЈ2ЃЉPHЉBE=1ЃЌРэгЩШчЯТЃК ЁпдкRtЁїABCжаЃЌAB=![]() ЃЌBC=3ЃЌ ЁргЩЙДЙЩЖЈРэЕУAC=2
ЃЌBC=3ЃЌ ЁргЩЙДЙЩЖЈРэЕУAC=2![]() ЃЌ
ЃЌ
ЁрCD=![]() ACЃЌ ЁрЁЯCAD=30Ёу ЁпADЁЮBCЃЌЁЯPFE=60ЁуЃЌ ЁрЁЯFPD=60ЁуЃЌ ЁрЁЯPHA=30Ёу=ЁЯCADЃЌ
ACЃЌ ЁрЁЯCAD=30Ёу ЁпADЁЮBCЃЌЁЯPFE=60ЁуЃЌ ЁрЁЯFPD=60ЁуЃЌ ЁрЁЯPHA=30Ёу=ЁЯCADЃЌ
ЁрPA=PHЃЌ ЁрЁїAPHЪЧЕШбќШ§НЧаЮЃЌ зїERЁЭADгкRЃЈШчЭМ2ЃЉ RtЁїPERжаЃЌЁЯRPE=60ЁуЃЌ ЁрPR=![]() PE=1ЃЌ
PE=1ЃЌ
ЁрPHЉBE=PAЉBE=PR=1ЃЎ
ЃЈ3ЃЉНсТлВЛГЩСЂЃЌ
ЕБ1ЃМCFЃМ2ЪБЃЌPH=1ЉBEЃЌ ЕБ2ЃМCFЃМ3ЪБЃЌPH=BEЉ1ЃЎ