题目内容
【题目】如图,在等边![]() 中,D为边AC的延长线上一点(
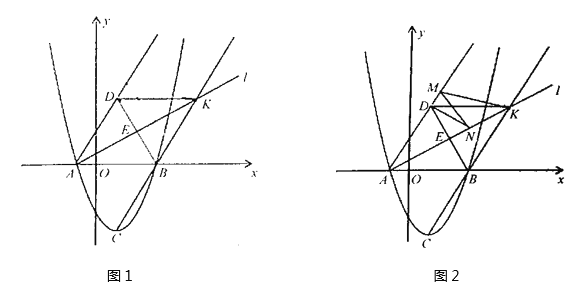
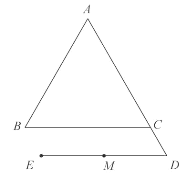
中,D为边AC的延长线上一点(![]() ),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
),平移线段BC,使点C移动到点D,得到线段ED,M为ED的中点,过点M作ED的垂线,交BC于点F,交AC于点G.
(1)依题意补全图形;
(2)求证:![]() ;
;
(3)连接DF并延长交AB于点H,用等式表示线段AH与CG的数量关系,并证明.
【答案】(1)见解析;(2)证明见解析;(3)线段AH与CG的数量关系:![]() .证明见解析.
.证明见解析.
【解析】
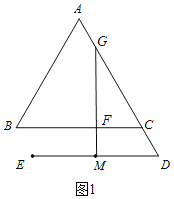
(1)补全的图形如图1所示;
(2)根据直角三角形含![]() 角的性质得:
角的性质得:![]() ,得
,得![]() ,即可证出;
,即可证出;
(3)作辅助线,证明四边形![]() 是平行四边形和
是平行四边形和![]() ,即可证出.
,即可证出.
(1)补全的图形如图1所示,
(2)证明:∵![]() 是等边三角形,
是等边三角形,
∴![]() .
.
![]() .
.
由平移可知![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
(3)线段AH与CG的数量关系:![]() .
.
证明:如图2,连接BE,EF.

∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形.
是平行四边形.
∴![]() ,
,![]() .
.
∵![]() 垂直平分
垂直平分![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目