题目内容
【题目】已知平面内有一个△ABC,O为平面内的一点,延长AO到A′,使OA′=OA,延长BO到B′,使OB′=OB,延长CO到从C′,使OC′=OC,得到△A′B′C′,问:△A′B′C′与△ABC是否全等?这两个三角形的对应边是否平行?请说明理由.
【答案】△A'B'C'≌△ABC,这两个三角形的对应边平行,理由见解析
【解析】
先根据题意画出图形,然后由条件即可分析推理出这两个三角形全等,并且对应边是平行的.
△A'B'C'≌△ABC,这两个三角形的对应边平行,理由如下:
如图所示,

在△AOC和△A'OC'中,
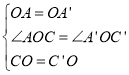 ,
,
∴△AOC≌△A'OC'(SAS),
∴AC=A'C',
同理可得△BOC≌△B'OC',△AOB≌△A'OB',
∴BC=B'C',AB=A'B',
在△ABC和△A'B'C'中,
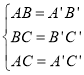 ,
,
∴△ABC≌△A'B'C'(SSS),
∵△AOC≌△A'OC',
∴∠CAO=∠C'A'O,
∴AC∥A'C',
同理可得AB∥A'B',BC∥B'C'.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目