题目内容
【题目】已知![]() 为
为![]() 斜边
斜边![]() 上的高,以
上的高,以![]() 为直径的圆交
为直径的圆交![]() 于
于![]() 点,交
点,交![]() 于
于![]() 点,
点,![]() 为
为![]() 的中点.
的中点.
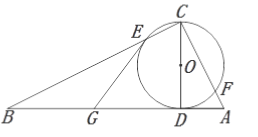
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]()
【解析】
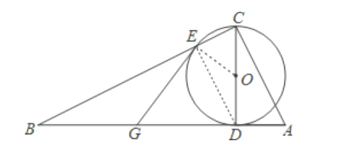
(1)连DE、OE,利用圆周角定理可得∠CED=∠BED=90°,因为G为BD的中点,由直角三角形的性质可得GE=GD,再由OE=OD,易得∠OED=∠ODE,可得∠GEO=∠GDO,由CD⊥AB,可得∠GEO=∠GDO=90°,可得结论;
(2)首先由垂直的定义易得∠B=∠ACD,利用锐角三角函数可得tanB=![]() 可知CD=GD=DE=
可知CD=GD=DE=![]() BD,根据tanB=tan∠ACD,列比例式
BD,根据tanB=tan∠ACD,列比例式![]() 即可求得答案.
即可求得答案.
解:(1)证明:连![]() ,
,
∵![]() 为
为![]() 的直径,
的直径,
∴![]() ,
,
∵![]() 为
为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 为
为![]() 的切线;
的切线;
(2)∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]()
∵![]() , EG= DG= BG= CD=
, EG= DG= BG= CD=![]() BD
BD
∴![]()
∴![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目