Question

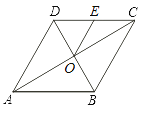
【题目】如图，在△ABC中，AB＝AC＝5，BC＝8，点D是边BC上一点（点D不与点B，C重合），将△ACD沿AD翻折，点C的对应点是E，AE交BC于点F，若DE∥AB，则DF的长为___．

Answer 1

【答案】.

【解析】

由等腰三角形的性质和平行线的性质得出∠B＝∠C，∠BAF＝∠E，∠B＝∠EDF，由折叠的性质得：∠E＝∠C，AE＝AC＝5，ED＝CD，得出∠B＝∠BAF＝∠E＝∠EDF，证出AF＝BF，EF＝DF，得出BD＝AF＝AC＝5ED＝CD＝BC﹣BD＝3，由平行线得出△EDF∽△ABF，得出比例式，即可得出结果．

AB＝AC＝5，

∴∠B＝∠C，

∵DE∥AB，

∴∠BAF＝∠E，∠B＝∠EDF，

由折叠的性质得：∠E＝∠C，AE＝AC＝5，ED＝CD，

∴∠B＝∠BAF＝∠E＝∠EDF，

∴AF＝BF，EF＝DF，

∴BD＝AF＝AC＝5，

∴ED＝CD＝BC﹣BD＝3，

∵DE∥AB，

∴△EDF∽△ABF，

∴，即，

解得：DF＝；

故答案为．