题目内容
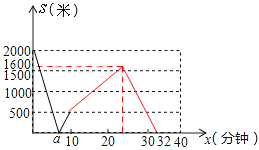
【题目】甲、乙两地之间有一条笔直的公路L,小明从甲地出发沿公路ι步行前往乙地,同时小亮从乙地出发沿公路L骑自行车前往甲地,小亮到达甲地停留一段时间,原路原速返回,追上小明后两人一起步行到乙地.设小明与甲地的距离为y1米,小亮与甲地的距离为y2米,小明与小亮之间的距离为s米,小明行走的时间为x分钟.y1、y2与x之间的函数图象如图1,s与x之间的函数图象(部分)如图2.
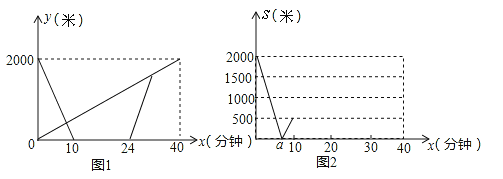
(1)求小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式;
(2)求小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式;
(3)在图2中,补全整个过程中s(米)与x(分钟)之间的函数图象,并确定a的值.
【答案】 (1) y1=﹣200x+2000。
(2) s=﹣150x+4800。
(3)详见解析
【解析】
(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由待定系数法根据图象就可以求出解析式。
(2)先根据函数图象求出甲乙的速度,然后与追击问题就可以求出小亮追上小明的时间,就可以求出小亮从甲地返回到与小明相遇的过程中s(米)与x(分钟)之间的函数关系式。
(3)先根据相遇问题建立方程就可以求出a值,10分钟甲、乙走的路程就是相距的距离,14分钟小明走的路程和小亮追到小明时的时间就可以补充完图象。
解:(1)设小亮从乙地到甲地过程中y1(米)与x(分钟)之间的函数关系式为y1=k1x+b,由图象,得:
![]() ,解得:
,解得:![]() 。
。
∴y1=﹣200x+2000。
(2)由题意,得小明的速度为:2000÷40=50米/分,小亮的速度为:2000÷10=200米/分,
∴小亮从甲地追上小明的时间为24×50÷(200﹣50)=8分钟,
∴24分钟时两人的距离为:s=24×50=1200;32分钟时S=0。
设s与x之间的函数关系式为:s=kx+b1,由题意,得
![]() ,解得:
,解得:![]() 。
。
∴s=﹣150x+4800。
(3)由题意,得a=2000÷(200+50)=8分钟,
当x=24时,s=1200;当x=32时,S=0。
故描出相应的点就可以补全图象如图: