题目内容
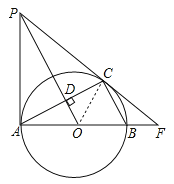
【题目】如图,AB、AC分别是⊙O的直径和弦,OD⊥AC于点D.过点A作⊙O的切线与
OD的延长线交于点P,PC、AB的延长线交于点F.
(1)求证:PC是⊙O的切线;
(2)若∠ABC=60°,AB=10,求线段CF的长.

【答案】(1)证明见解析(2)5![]()
【解析】
(1)连接OC,可以证得△OAP≌△OCP,利用全等三角形的对应角相等,以及切线的性质定理可以得到:∠OCP=90°,即OC⊥PC,即可证得;
(2)先证△OBC是等边三角形得∠COB=60°,再由(1)中所证切线可得∠OCF=90°,结合半径OC=5可得答案.
(1)连接OC.
∵OD⊥AC,OD经过圆心O,∴AD=CD,∴PA=PC.
在△OAP和△OCP中,∵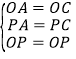 ,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP.
,∴△OAP≌△OCP(SSS),∴∠OCP=∠OAP.
∵PA是半⊙O的切线,∴∠OAP=90°,∴∠OCP=90°,即OC⊥PC,∴PC是⊙O的切线.
(2)∵OB=OC,∠OBC=60°,∴△OBC是等边三角形,∴∠COB=60°.
∵AB=10,∴OC=5.
由(1)知∠OCF=90°,∴CF=OCtan∠COB=5![]() .
.

 每课必练系列答案
每课必练系列答案【题目】为了发展学生的核心素养,培养学生的综合能力,某中学利用“阳光大课间”,组织学生积极参加丰富多彩的课外活动,学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等,其中射击队在某次训练中,甲、乙两名队员各射击10发子弹,成绩用如图的折线统计图表示:(甲为实线,乙为虚线)

(1)依据折线统计图,得到下面的表格:
射击次序(次) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
甲的成绩(环) | 8 | 9 | 7 | 9 | 8 | 6 | 7 | a | 10 | 8 |
乙的成绩(环) | 6 | 7 | 9 | 7 | 9 | 10 | 8 | 7 | b | 10 |
其中a= ,b= ;
(2)甲成绩的众数是 ,乙成绩的中位数是 环;
(3)请运用方差的知识,判断甲、乙两人谁的成绩更为稳定?
(4)该校射击队要参加市组织的射击比赛,已预选出2名男同学和2名女同学,现要从这4名同学中任意选取2名同学参加比赛,请用列表或画树状图法,求出恰好选到1男1女的概率.







