题目内容
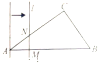
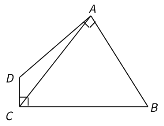
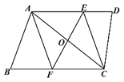
【题目】如图,矩形ABCD中,AB=5,BC=8,点P在AB上,AP=1.将矩形ABCD沿CP折叠,点B落在点B'处.B'P、B′C分别与AD交于点E、F,则EF=_____.
【答案】![]()
【解析】
过P作PG⊥CD于G,交CB′于H,根据矩形的性质得到AD=PG=BC=8,DG=AP=1,求得CG=PB=4,根据折叠的性质得到∠BCP=∠PCH,根据平行线的性质得到∠HPC=∠PCB,等量代换得到∠HPC=∠PCH,求得HP=CH,设HG=x,则CH=PH=8﹣x,根据勾股定理得到CH=PH=5,根据相似三角形的性质即可得到结论.
过P作PG⊥CD于G,交CB′于H,
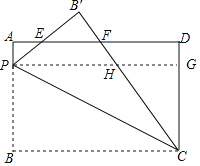
则四边形ADGP和四边形PBCG是矩形,
∴AD=PG=BC=8,DG=AP=1,
∴CG=PB=4,
∵将矩形ABCD沿CP折叠,点B落在点B'处,
∴∠BCP=∠PCH,
∵PG∥BC,
∴∠HPC=∠PCB,
∴∠HPC=∠PCH,
∴HP=CH,
设HG=x,则CH=PH=8﹣x,
∵HG2+CG2=CH2,
∴x2+42=(8﹣x)2,
∴x=3,
∴CH=PH=5,
∵HG∥DF,
∴△CHG∽△CFD,
∴![]() ,
,
∴![]() ,
,
∴CF=![]() ,DF=
,DF=![]() ,
,
∴B′F=![]() ,
,
∵∠B′=∠D=90°,∠EFB′=∠DFC,
∴△B′EF∽△DCF,
∴![]() ,
,
∴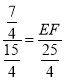 ,
,
∴EF=![]() .
.
故答案为![]() .
.

 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案【题目】为了鼓励城市周边的农民的种菜的积极性,某公司计划新建![]() ,
,![]() 两种温室80栋,将其售给农民种菜.已知建1个
两种温室80栋,将其售给农民种菜.已知建1个![]() 型温室和2个
型温室和2个![]() 型温室一共需要8.1万元,两种温室的成本和出售价如下表:
型温室一共需要8.1万元,两种温室的成本和出售价如下表:
|
| |
成本(万元/栋) | 2.5 |
|
出售价(万元/栋) | 3.1 | 3.5 |
(1)求![]() 的值;
的值;
(2)已知新建![]() 型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?
型温室不少于38栋不多于50栋且所建的两种温室可全部售出.为了减轻菜农负担,试问采用什么方案建设温室可使利润最少,最少利润是多少?