题目内容
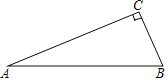
【题目】如图,已知△ABC,且∠ACB=90°.
(1)请用直尺和圆规按要求作图(保留作图痕迹,不写作法和证明):
①以点A为圆心,BC边的长为半径作⊙A;
②以点B为顶点,在AB边的下方作∠ABD=∠BAC.
(2)请判断直线BD与⊙A的位置关系,并说明理由.
【答案】(1)详见解析;(2)直线BD与⊙A相切,理由详见解析.
【解析】
(1)①以点A为圆心,以BC的长度为半径画圆即可;
②以点A为圆心,以任意长为半径画弧,与边AB、AC相交于两点E、F,再以点B为圆心,以同等长度为半径画弧,与AB相交于一点M,再以点M为圆心,以EF长度为半径画弧,与前弧相交于点N,作射线BN即可得到∠ABD;
(2)根据内错角相等,两直线平行可得AC∥BD,再根据平行线间的距离相等可得点A到BD的距离等于BC的长度,然后根据直线与圆的位置关系判断直线BD与⊙A相切.
解:(1)如图所示;
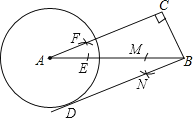
(2)直线BD与⊙A相切.
∵∠ABD=∠BAC,
∴AC∥BD,
∵∠ACB=90°,⊙A的半径等于BC,
∴点A到直线BD的距离等于BC,
∴直线BD与⊙A相切.

练习册系列答案
相关题目