Question

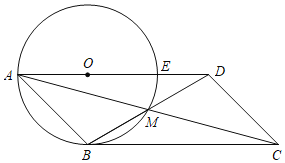
【题目】如图，点E在△ABC的边AB上，过点B，C，E的⊙O切AC于点C．直径CD交BE于点F，连结BD，DE．已知∠A=∠CDE，AC=2，BD=1．

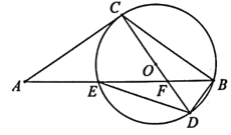
（1）求⊙O的直径.

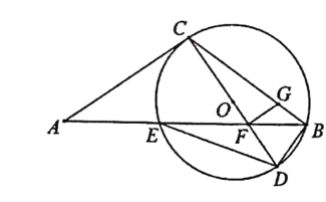
（2）过点F作FG⊥CD交BC于点G，求FG的长.

Answer 1

【答案】（1）3；（2）

【解析】

（1）因为CD是⊙O的直径，所以∠CBD=90°，因为∠A=∠CDE=∠CBA，可得BC=AC=2，因为BD=1，在Rt△CBD中，用勾股定理即可得出⊙O的直径；

（2）由题意，可得FG∥AC，所以∠GFB=∠CAB=∠CBA，即FG=GB=x，根据sin∠BCD=，得CG=3FG=3x，由BC=2可列方程：x+3x=2，解得x的值即可得出FG的长．

（1）∵CD是⊙O的直径，

∴∠CBD=90°，

∵∠A=∠CDE，∠CDE=∠CBA，

∴∠CAB=∠CBA，

∴BC=AC=2，

∵BD=1，

∴⊙O的直径CD=；

（2）如图，∵过点B，C，E的圆O切AC于点C，直径CD交BE于点F，

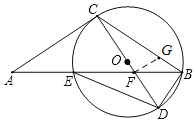
∴AC⊥CD，

∵FG⊥CD，

∴FG∥AC，

∴∠GFB=∠CAB=∠CBA，

∴FG=GB=x，

∵sin∠BCD=，

∴，即CG=3FG=3x，

∵BC=2，

∴x+3x=2，

∴FG=x=．