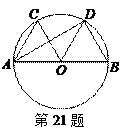题目内容
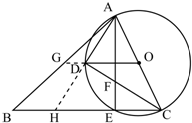
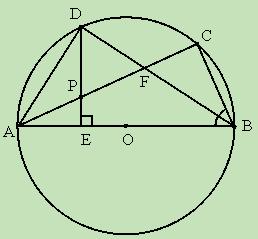
(2011•桂林)如图,在锐角△ABC中,AC是最短边;以AC中点O为圆心, AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
(1)求证:D是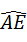 的中点;
的中点;
(2)求证:∠DAO=∠B+∠BAD;
(3)若 ,且AC=4,求CF的长.
,且AC=4,求CF的长.
 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.(1)求证:D是
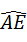 的中点;
的中点;(2)求证:∠DAO=∠B+∠BAD;
(3)若
 ,且AC=4,求CF的长.
,且AC=4,求CF的长.
证明:(1)∵AC是⊙O的直径,
∴AE⊥BC,
∵OD∥BC,
∴AE⊥OD,
∴D是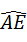 的中点;
的中点;
(2)方法一:
如图,延长OD交AB于G,则OG∥BC,
∴∠AGD=∠B,
∵∠ADO=∠BAD+∠AGD,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠DAO=∠B+∠BAD;
方法二:
如图,延长AD交BC于H,
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠DAO=∠B+∠BAD;
(3)∵AO=OC,
∴S△OCD= S△ACD,
S△ACD,
∵ ,
,
∴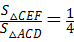 ,
,
∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴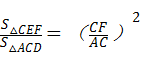 ,
,
即: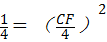 ,
,
∴CF=2.
∴AE⊥BC,
∵OD∥BC,
∴AE⊥OD,
∴D是
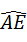 的中点;
的中点;(2)方法一:
如图,延长OD交AB于G,则OG∥BC,
∴∠AGD=∠B,
∵∠ADO=∠BAD+∠AGD,
又∵OA=OD,
∴∠DAO=∠ADO,
∴∠DAO=∠B+∠BAD;
方法二:
如图,延长AD交BC于H,
则∠ADO=∠AHC,
∵∠AHC=∠B+∠BAD,
∴∠ADO=∠B+∠BAD,
又∵OA=OD,
∴∠DAO=∠B+∠BAD;
(3)∵AO=OC,
∴S△OCD=
 S△ACD,
S△ACD,∵
 ,
,∴
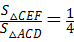 ,
,∵∠ACD=∠FCE,∠ADC=∠FEC=90°,
∴△ACD∽△FCE,
∴
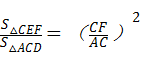 ,
,即:
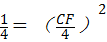 ,
,∴CF=2.

(1)由AC是⊙O的直径,即可求得OD∥BC,又由AE⊥OD,即可证得D是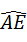 的中点;
的中点;
(2)首先延长OD交AB于G,则OG∥BC,可得OA=OD,根据等腰三角形的性质,即可求得∠DAO=∠B+∠BAD;
(3)由AO=OC,S△OCD= S△ACD,即可得
S△ACD,即可得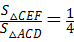 ,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
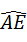 的中点;
的中点;(2)首先延长OD交AB于G,则OG∥BC,可得OA=OD,根据等腰三角形的性质,即可求得∠DAO=∠B+∠BAD;
(3)由AO=OC,S△OCD=
 S△ACD,即可得
S△ACD,即可得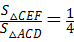 ,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
,又由△ACD∽△FCE,根据相似三角形的面积比等于相似比的平方,即可求得CF的长.
练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
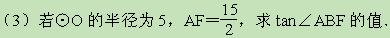 .
.
 ,求DE的长.
,求DE的长.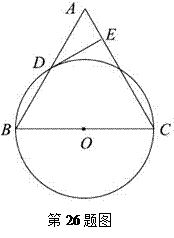
 为
为 外接圆的直径,
外接圆的直径, ,垂足为点
,垂足为点 ,
, 的平分线交
的平分线交 ,连接
,连接 ,
, .
. ;
;  ,
, 三点是否在以
三点是否在以 为圆心,以
为圆心,以 为半径的圆上?并说明理由.
为半径的圆上?并说明理由.
 ,∠COD=60°.
,∠COD=60°.