题目内容
如图,点D为AC上一点,点O为边AB上一点,AD=DO.以O为圆心,OD长为半

径作圆,交AC于另一点E,交AB于点F,G,连接EF.若
∠BAC=22°,则∠EFG=_ ▲ .

径作圆,交AC于另一点E,交AB于点F,G,连接EF.若
∠BAC=22°,则∠EFG=_ ▲ .
33°
连接OE,利用三角形的外角性质得出∠ODC的度数,再求出∠DOC,从而求出∠EOG的度数,再利用圆周角定理求出∠EFG的度数.
解:连接EO,

∵AD=DO,
∴∠BAC=∠DOA=22°,
∴∠EDO=44°,
∵DO=EO,
∴∠OED=∠ODE=44°,
∴∠DOE=180°-44°-44°=92°,
∴∠EOG=180°-92°-22°=66°,
∴∠EFG=1/2∠EOG=33°,
故答案为:33°.
解:连接EO,

∵AD=DO,
∴∠BAC=∠DOA=22°,
∴∠EDO=44°,
∵DO=EO,
∴∠OED=∠ODE=44°,
∴∠DOE=180°-44°-44°=92°,
∴∠EOG=180°-92°-22°=66°,
∴∠EFG=1/2∠EOG=33°,
故答案为:33°.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
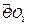 和
和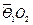 ,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧
,顶点O所经过的路程是这两段圆弧的长度之和,并且这两段圆弧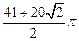 ?
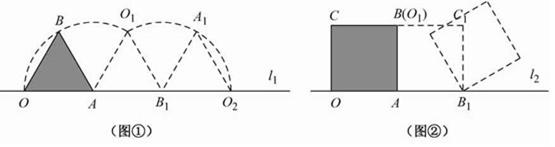
?
 AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.
AC长为半径作⊙O,交BC于E,过O作OD∥BC交⊙O于D,连接AE、AD、DC.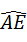 的中点;
的中点; ,且AC=4,求CF的长.
,且AC=4,求CF的长.
 中,
中,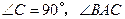 的角平分线
的角平分线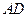 交
交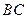 边于
边于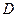 .
.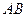 边上一点
边上一点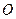 为圆心,过
为圆心,过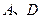 两点作
两点作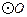 (不写作法,保留作图痕迹),再判断直线
(不写作法,保留作图痕迹),再判断直线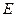 ,
,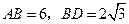 ,求线段
,求线段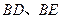 与劣弧
与劣弧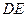 所围成的图形面积.(结果保留根号和
所围成的图形面积.(结果保留根号和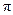 )
)
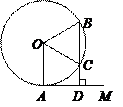
 ,以
,以 为直径,
为直径, 为圆心的半圆交
为圆心的半圆交 于点
于点 ,点
,点 为
为
 的中点,连接
的中点,连接 交
交 ,
, 为
为 的角平分线,且
的角平分线,且 ,垂足为点
,垂足为点 。
。
 是半圆
是半圆 ,
, ,求
,求 内接于圆
内接于圆 ,
, ,
, ,
, 是圆
是圆 于点
于点 ,连结
,连结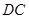 ,则
,则 等于
等于



