题目内容
【题目】如图,反比例函数y= ![]() 的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y=
的图象上有一动点A,连接AO并延长交图象的另一支于点B,在第二象限内有一点C,满足AC=BC,当点A运动时,点C始终在函数y= ![]() 的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 .
的图象上运动,tan∠CAB=2,则关于x的方程x2﹣5x+k=0的解为 . 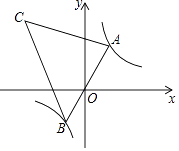
【答案】x1=﹣1,x2=6
【解析】解:连接OC,过点A作AE⊥y轴于点E,过点C作CF⊥y轴于点F,如图所示, 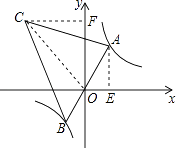
∵由直线AB与反比例函数y= ![]() 的对称性可知A、B点关于O点对称,
的对称性可知A、B点关于O点对称,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴ ![]() ,
,
∵tan∠CAB= ![]() =2,
=2,
∴CF=2AE,OF=2OE.
又∵AEOE= ![]() ,CFOF=|k|,
,CFOF=|k|,
∴k=±6.
∵点C在第二象限,
∴k=﹣6,
∴关于x的方程x2﹣5x+k=0可化为x2﹣5x﹣6=0,解得x1=﹣1,x2=6.
所以答案是:x1=﹣1,x2=6.
【考点精析】解答此题的关键在于理解解直角三角形的相关知识,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).

练习册系列答案
相关题目