Question

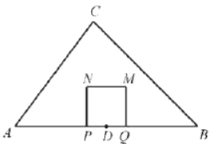
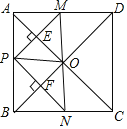
【题目】如图，在正方形ABCD中，点P是AB上一动点（不与A，B重合），对角线AC、BD相交于点O，过点P分别作AC、BD的垂线，分别交AC、BD于点E、F，交AD、BC于点M、N．下列结论：①△APE≌△AME；②PM+PN＝AC；③△POF∽△BNF；④当△PMN∽△AMP时，点P是AB的中点，其中一定正确的结论有_____．（填上所有正确的序号）．

Answer 1

【答案】①②④．

【解析】

①根据正方形的每一条对角线平分一组对角可得∠PAE=∠MAE=45°，然后利用“角边角”证明△APE和△AME全等；②根据全等三角形对应边相等可得，同理，，证出四边形PEOF是矩形，得出PF=OE，证得△APE为等腰直角三角形，得出AE=PE，PE+PF=OA，即可得到PM+PN=AC；

③判断出△POF不一定等腰直角三角形，△BNF是等腰直角三角形，从而确定出两三角形不一定相似；④证出△APM和△BPN以及△APE、△BPF都是等腰直角三角形，从而得出结论．

∵四边形ABCD是正方形，

∴∠BAC＝∠DAC＝45°．

∵PM⊥AC，

∴∠AEP=∠AEM=90°，

在△APE和△AME中，

，

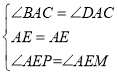∴△APE≌△AME（ASA），故①正确；

∴，

同理，．

∵正方形ABCD中，AC⊥BD，

又∵PE⊥AC，PF⊥BD，

∴∠PEO＝∠EOF＝∠PFO＝90°，且△APE中AE＝PE

∴四边形PEOF是矩形．

∴PF＝OE，

∵在△APE中，∠AEP=90°，∠PAE=45°，

∴△APE为等腰直角三角形，

∴AE=PE，

∴PE+PF＝OA，

又∵，，，

∴PM+PN＝AC，故②正确；

∵△BNF是等腰直角三角形，而△POF不一定是，

∴△POF与△BNF不一定相似，故③错误；

∵△AMP是等腰直角三角形，当△PMN∽△AMP时，△PMN是等腰直角三角形．

∴PM＝PN，

又∵△AMP和△BPN都是等腰直角三角形，

∴AP＝BP，即P是AB的中点．故④正确．

故答案为：①②④．