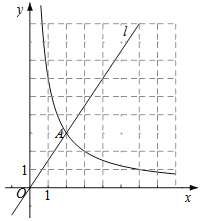题目内容
【题目】已知抛物线![]() ,
,![]() ,直线
,直线![]() .
.
(1)若该抛物线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,求该抛物线的顶点坐标;
,求该抛物线的顶点坐标;
(2)证明:该抛物线与直线![]() 必有两个交点;
必有两个交点;
(3)若该抛物线经过点![]() ,且对任意实数
,且对任意实数![]() ,不等式
,不等式![]() 都成立;当
都成立;当![]() 时,该二次函数的最小值为
时,该二次函数的最小值为![]() .求直线
.求直线![]() 的解析式.
的解析式.
【答案】(1)该抛物线的顶点坐标为![]() ;(2)证明见解析;(3)直线l的解析式为y=-x+1或
;(2)证明见解析;(3)直线l的解析式为y=-x+1或![]() .
.
【解析】
(1)抛物线与![]() 轴交点的纵坐标为
轴交点的纵坐标为![]() ,即:
,即:![]() ,解得:
,解得:![]() ,即可求解;
,即可求解;
(2)联立抛物线和直线的表达式得:x2-(k+3m)x-4=0,判断![]() ,即可证明;
,即可证明;
(3)分![]() 、
、![]() 、
、![]() 三种情况,分别求解即可.
三种情况,分别求解即可.
(1)依题意可知![]() ,
,
则![]() ,
,
∴该抛物线对应的函数解析式为![]() ,
,
∴该抛物线的顶点坐标为![]() .
.
(2)证明:将![]() 代入
代入![]() ,
,
整理得:![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() [-(k+3m)]2-4×(-4)=(k+3m)2+16>0,
[-(k+3m)]2-4×(-4)=(k+3m)2+16>0,
∴该抛物线与直线l必有两个交点;
(3)由抛物线经过点(t,-4),且对任意实数x,不等式![]() 都成立,
都成立,
得抛物线![]() 的最小值为-4.
的最小值为-4.
∵![]()
![]()
![]() ,
,
∴![]() ,
,
整理得3m2+2m-5=0,解得:m=1或![]()
∵![]() ,
,
∴![]() ,
,![]() 舍去,
舍去,
当m=1时,抛物线的解析式为![]() ,
,
此时抛物线的对称轴为直线![]() ,
,
①当k<1时,抛物线在![]() 上,函数值y随x的增大而减小,
上,函数值y随x的增大而减小,
∴当x=k时,![]() ,
,
∴![]() ,
,
解得:![]() 或k=2(舍去),
或k=2(舍去),
直线l的解析式为![]() ;
;
②当![]() 时,即
时,即![]() ,抛物线在
,抛物线在![]() 上,
上,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
直线l的解析式为![]() ;
;
③当![]() 时,即
时,即![]() 时,抛物线在
时,抛物线在![]() 上,函数值y随x的增大而增大,
上,函数值y随x的增大而增大,
∴当x=k-2时,![]() =(k-2)2-2(k-2)-3,
=(k-2)2-2(k-2)-3,
∴(k-2)2-2(k-2)-3=-2k+1,
解得:k1=k2=2,
与k-2>1矛盾,不符合题意,
综上,直线l的解析式为y=-x+1或![]() .
.

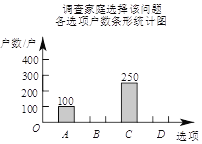
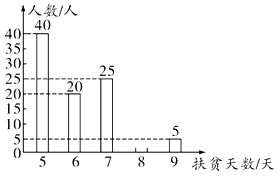
【题目】光明中学全体学生900人参加社会实践活动,从中随机抽取50人的社会实践活动成绩制成如图所示的条形统计图,结合图中所给信息解答下列问题:
![]() 填写下表:
填写下表:
中位数 | 众数 | |
随机抽取的50人的社会实践活动成绩 |
![]() 估计光明中学全体学生社会实践活动成绩的总分.
估计光明中学全体学生社会实践活动成绩的总分.