Question

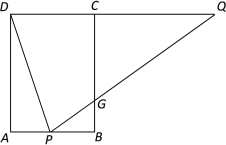
【题目】如图，矩形ABCD中，AB＝4，AD＝6，点P在AB上，点Q在DC的延长线上，连接DP，QP，且∠APD＝∠QPD，PQ交BC于点G.

（1）求证：DQ＝PQ；

（2）求AP·DQ的最大值；

（3）若P为AB的中点，求PG的长.

Answer 1

【答案】（1）证明见解析；（2）26；（3）

【解析】试题分析：（1）要证DQ＝PQ，即证∠QPD＝∠QDP，又因为已知∠APD＝∠QPD，即证∠APD＝∠QDP，即证AB∥CD，由四边形ABDF是矩形得到AB∥CD；（2）过点Q作QE⊥DP，垂足为E，则DE＝DP，先证△QDE∽△DPA，

得出＝， 所以AP·DQ＝DP·DE＝DP2，在Rt△DAP中，有DP2＝DA2＋AP2＝36＋AP2，所以AP·DQ＝（36＋AP2），又由点P在AB上，故AP≤4，所以AP·DQ≤26，即AP·DQ的最大值为26；（3）由P为AB的中点得到AP＝BP＝AB＝2，由（2）得，DQ＝（36＋22）＝10，所以CQ＝DQ－DC＝6．设CG＝x，则BG＝6－x，由（1）得，DQ∥AB，所以＝，即＝，解得x＝，所以BG＝6－＝，所以PG＝＝．

试题解析：

（1）∵四边形ABDF是矩形，

∴AB∥CD，

∴∠APD＝∠QDP．

∵∠APD＝∠QPD，

∴∠QPD＝∠QDP，

∴DQ＝PQ．

（2）过点Q作QE⊥DP，垂足为E，则DE＝DP，如图所示：

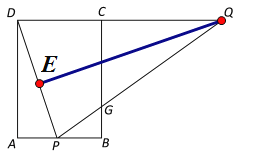
∵∠DEQ＝∠PAD＝90°，∠QDP＝∠APD，

∴△QDE∽△DPA，

∴＝，

∴AP·DQ＝DP·DE＝DP2．

在Rt△DAP中，有DP2＝DA2＋AP2＝36＋AP2，

∴AP·DQ＝（36＋AP2）．

∵点P在AB上，

∴AP≤4，

∴AP·DQ≤26，即AP·DQ的最大值为26．

（3）∵P为AB的中点，

∴AP＝BP＝AB＝2，

由（2）得，DQ＝（36＋22）＝10．

∴CQ＝DQ－DC＝6．设CG＝x，则BG＝6－x，

由（1）得，DQ∥AB，

∴＝，

即＝，解得x＝，

∴BG＝6－＝，

∴PG＝＝．