题目内容
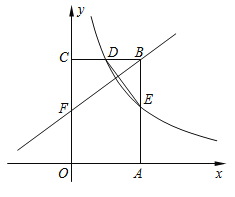
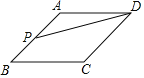
【题目】如图,![]() 水平放在平面直角坐标系中,点
水平放在平面直角坐标系中,点![]() 的坐标分别为
的坐标分别为![]() ,点
,点![]() 在函数
在函数![]() 的图象上.
的图象上.

![]() 求函数
求函数![]() 的表达式;
的表达式;
![]() 求点
求点![]() 的坐标;
的坐标;
![]() 将
将![]() 沿
沿![]() 轴正方向平移
轴正方向平移![]() 个单位后,判断点
个单位后,判断点![]() 能否落在函数
能否落在函数![]() 的图象上,请说明理由.
的图象上,请说明理由.
【答案】(1)y=![]() ;(2)C点坐标为(5,1);(3)点C落在函数y=
;(2)C点坐标为(5,1);(3)点C落在函数y=![]() (k>0)的图象上.
(k>0)的图象上.
【解析】
(1)将点![]() 代入函数
代入函数![]() 即可求k的值,即可得到此函数的解析式;
即可求k的值,即可得到此函数的解析式;
(2)根据![]() 水平放在平面直角坐标系中,可得点C的纵坐标与点D的纵坐标相同,且AB=CD,求出AB的长便可得到DC的长,从而可计算求点C的横坐标;
水平放在平面直角坐标系中,可得点C的纵坐标与点D的纵坐标相同,且AB=CD,求出AB的长便可得到DC的长,从而可计算求点C的横坐标;
(3)先计算出点C向右平移10个单位后的坐标,然后看此坐标值是否满足函数![]() 的解析式,如满足,则在此函数图像上,反之,则不在其图像上.
的解析式,如满足,则在此函数图像上,反之,则不在其图像上.
解:(1)把点B(3,5)代入y=![]() (k>0),
(k>0),
∴k=3×5=15,
∴反比例函数解析式为y=![]() ;
;
(2)∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵点A、D的坐标分别为(﹣2,5)、(0,1),点B(3,5),
∴AB=3+2=5,∴CD=5,
∴C点坐标为(5,1);
(3)点C落在函数y=![]() (k>0)的图象上.
(k>0)的图象上.
理由如下:
把点(5,1)沿x轴正方向平移10个单位后得到对应点的坐标为(15,1),
而x=15时,y=![]() =1,
=1,
∴点C落在函数y=![]() (k>0)的图象上.
(k>0)的图象上.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目