题目内容
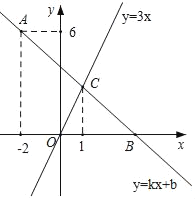
【题目】如图，直线
与反比例函数
的图像交于点
，与
轴交于点
，与
轴交于点
．
（1）求
的值和反比例函数的表达式；
（2）在轴上有一动点
，过点
作平行于轴的直线，交反比例函数的图像于点
，交直线
于点
，连接
．若
，求
的值．
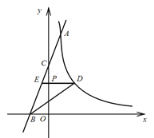
【答案】（1）9；
（2）n无解，理由见解析
【解析】
（1）将点A的坐标代入直线
中即可求出m的值，然后再将A点代入反比例函数表达式
中即可得出反比例函数的表达式；
（2）先根据直线求出点B,C的坐标，进而求出
，则可求
，然后根据P点坐标表示出D,E的坐标，进而表示出，然后建立一个关于n的方程，解方程即可．
解：（1）将
代入直线中，得
．
．
将
代入中，得
．
反比例函数的解析式为．
（2）令
时，
；令
时，则
，解得
，
∴
，
，
，
，
．
，
轴，
，
．
．
．
解得，
，
．
∴，都不符合题意，舍去，
∴n无解．
【题目】若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照学习函数的过程与方法，探究分段函数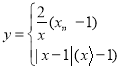
的图象与性质．列表：
x | … |
|
|
|
|
|
| 0 |
| 1 |
| 2 |
| 3 | … |
y | … |
|
| 1 |
| 2 |
| 1 |
| 0 |
| 1 |
| 2 | … |
描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示．
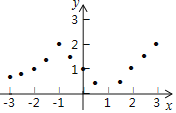
（1）如图，在平面直角坐标系中，观察描出的这些点的分布，作出函数图象；
（2）研究函数并结合图象与表格，回答下列问题：
①点
，
，
，
在函数图象上，
，
；（填“＞”，“＝”或“＜”）
②当函数值
时，求自变量x的值；
③在直线
的右侧的函数图象上有两个不同的点
，
，且
，求
的值；
④若直线
与函数图象有三个不同的交点，求a的取值范围．
【题目】某体育用品商店销售A，B两种型号的运动鞋，这两种运动鞋的进价与售价如下表，2018年第一季度的总利润为50 000元，其各月份的月利润占季度总利润的百分比如下图.
两种运动鞋的进价与售价表
A型号运动鞋 | B型号运动鞋 | |
进价（元/双） | 200 | 220 |
售价（元/双） | 250 | 280 |
（1）1月份的销售利润为 元；2月份的销售利润为 元，3月份的销售利润为_________元.
（2）如果A型运动鞋的2月份销量比1月份提高了20%，B型运动鞋的2月份销量是1月份的1.5倍，求1月份A、B两种运动鞋的销售量.
（3）已知3月份A型运动鞋的销售量超过B型运动鞋的销售量，问最多可能卖出B型运动鞋多少双.
