��Ŀ����
����Ŀ��ij������ɲ������ʻ�ľ���s(��λ����)��ʱ��t(��λ����)֮��Ĺ�ϵ�ò����������±���
ʱ��t(��) | 0 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | �� |
��ʻ����s(��) | 0 | 2.8 | 5.2 | 7.2 | 8.8 | 10 | 10.8 | �� |
�������ֱ仯����һֱ����������ֹͣ��
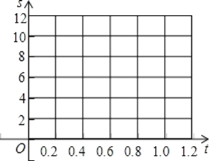
(1)������Щ�����ڸ���������ϵ�л�����Ӧ�ĵ㣻
(2)ѡ���ʵ��ĺ�����ʾs��t֮��Ĺ�ϵ�������Ӧ�ĺ�������ʽ��
(3)��ɲ����������ʻ�˶�����ֹͣ?
�ڵ�t�ֱ�Ϊt1,t2(t1<t2)ʱ,��Ӧs��ֵ�ֱ�Ϊs1,s2,��Ƚ�![]() ��
��![]() �Ĵ�С��
�Ĵ�С��
���𰸡���1������������2��![]() ����3����
����3����![]() �ף���
�ף���![]() ��
��![]()
��������
��1����㣬��ƽ���������Ӽ��ɣ�
��2��������κ�������ʽ����3������������ɵö��κ�������ʽ�������ٰ�����ĵ������֤�Ƿ��ڶ��κ����ϣ�
��3����������ɲ��ʱ���ʱֹͣ�����ù�ʽ������ϣ�2���õ��ĺ�������ʽ�������Ӧ����ֵ���ɣ�
�ڷֱ������������ʽ��ֵ����������ʱ��Ĵ�С���Ƚϼ��ɣ�
(1)���ͼ��ʾ��
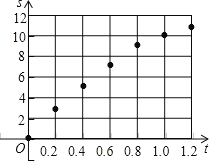
(2)��ɢ��ͼ��֪�ú���Ϊ���κ���
����κ����Ľ���ʽΪ��s=at2+bt+c��
�������߾�����(0,0)��
��c=0��
���ɵ�(0.2,2.8),(1,10)�ɵã�
![]()
��ã�a=5��b=15��
����κ����Ľ���ʽΪ��s=5t2+15t��
������,����������s=5t2+15t��.
(3)������ɲ����ֹͣʱ�ľ��뼴�������е������룬
��t=![]() =
=![]() ʱ,���о������,S=
ʱ,���о������,S=![]() =
=![]() =
=![]() ��
��
��ɲ����������ʻ��![]() �ײ�ֹͣ.
�ײ�ֹͣ.
�ڡ�s=5t2+15t,
��![]() ,
,![]()
��![]()
ͬ��![]() ��
��
��t1<t2��
��![]() ��
��![]()

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�