��Ŀ����
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC=30������һֱ�����ǰ壨��M=30������ֱ�Ƕ�����ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
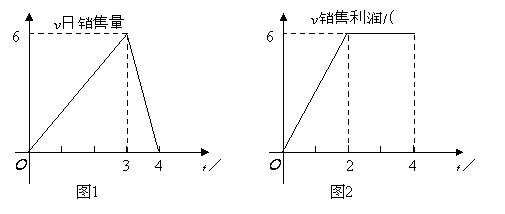
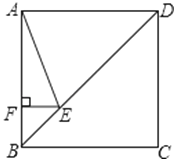
(1)��ͼ1�е����ǰ��Ƶ�O��ÿ��3�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ2������t���OMǡ��ƽ�֡�BOC����t=�� ����ֱ��д�����
(2)��(1)�ʵĻ����ϣ������ǰ���ת����ͬʱ������OCҲ��O����ÿ��6�����ٶ���˳ʱ�뷽����תһ�ܣ���ͼ3����ô�����������OCƽ�֡�MON����˵�����ɣ�
(3)��(2)�ʵĻ����ϣ���ô�����������MOC=36������˵�����ɣ�

���𰸡���1��5����2��5��ʱOCƽ����MON�����������������3���������.
��������
��1���������̼��ɽ�����⣻
��2��������MOC=45��������������⼴�ɣ�
��3�����ݡ�AON+��BOM=90������BOC=��COM�����AONΪ3t����AOCΪ30��+6t���ٸ��������г�������⼴��.
��1���١ߡ�AON+��BOM=90�㣬��COM=��MOB��
�ߡ�AOC=30�㣬
���BOC=2��COM=150�㣬
���COM=75�㣬
���CON=15�㣬
���AON=��AOC����CON=30�㩁15��=15�㣬
��ã�t=15���3��=5�룻
���ǣ��������£�
�ߡ�CON=15�㣬��AON=15�㣬
��ONƽ����AOC��
��2��5��ʱOCƽ����MON���������£�
�ߡ�AON+��BOM=90�㣬��CON=��COM��
�ߡ�MON=90�㣬
���CON=��COM=45�㣬
�����ǰ��Ƶ�O��ÿ��3�����ٶȣ�����OCҲ��O����ÿ��6�����ٶ���ת��
����AONΪ3t����AOCΪ30��+6t��
�ߡ�AOC����AON=45�㣬
�ɵã�6t��3t=15�㣬
��ã�t=5�룻
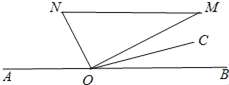
��3������ͼ��OCƽ����MOB
�ߡ�AON+��BOM=90�㣬��BOC=��COM��
�����ǰ��Ƶ�O��ÿ��3�����ٶȣ�����OCҲ��O����ÿ��6�����ٶ���ת��
����AONΪ3t����AOCΪ30��+6t��
���COMΪ![]() ��90�㩁3t����
��90�㩁3t����
�ߡ�BOM+��AON=90�㣬
�ɵã�180�㩁��30��+6t��=![]() ��90�㩁3t����
��90�㩁3t����
��ã�t=![]() �룻
�룻
�𣺾���![]() ����MOC=36�㣮
����MOC=36�㣮