题目内容
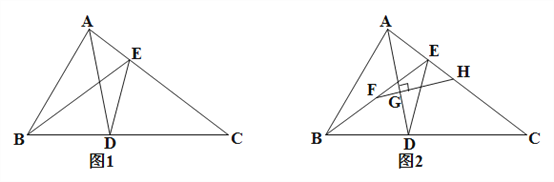
【题目】在ΔABC中点D为BC上一点,E为AC上一点,连接AD、BE、DE,已知BD=DE,AD=DC,∠ADB=∠CDE.
(1)如图1,若∠ACB=40°时,求∠BAC的度数.
(2)如图2,F是BE的中点,过点F作AD的垂线,分别交AD、AC于点G、H,求证:AH=CH.
【答案】(1)80°;(2)证明见解析
【解析】试题分析:(1)易证ΔADB≌ΔCDE,得∠ACB=∠DAC=∠DAB=40°,故∠BAC=80°;
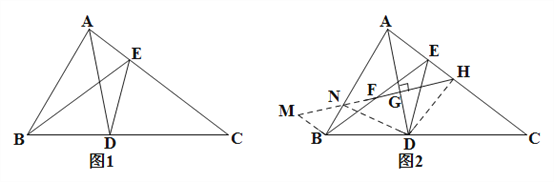
(2)延长HF至点M使FM=FH,交AB于点N,连接BM、DH、DN,得ΔBMF≌ΔEHF,得BM=EH,∠EHF=∠M,结合(1)的结论可证明ΔAGN≌ΔAGH得BM=BN=EH,利用线段垂直平分线的性质得DN=DH ∠ADN=∠ADH,从而可证ΔBDN≌ΔEDH,继而证出∠ADH=∠CDH,进一步得出:AH=CH
试题解析:
简要过程:
(1)∵ΔADB≌ΔCDE (SAS)
∴∠ACB=∠DAC=∠DAB=40°
∴∠BAC=80°
(2)延长HF至点M使FM=FH,交AB于点N,连接BM、DH、DN
∴ΔBMF≌ΔEHF
∴BM=EH,∠EHF=∠M
由①得∠DAC=∠DAB,且FH⊥AD
∴ΔAGN≌ΔAGH
∴∠ANG=∠AHG
∵∠ANG=∠BNM
∴∠M=∠BNM
∴BM=BN=EH
∵ΔADN≌ΔADH(或用中垂线的性质)
∴DN=DH ∠ADN=∠ADH
∴ΔBDN≌ΔEDH(SSS)
∴∠BDN=∠EDH
∴∠ADB-∠BDN=∠CDE-∠EDH
∴∠ADN=∠CDH
∴∠ADH=∠CDH
∴AH=CH

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目