题目内容
【题目】如图，长方形纸片CD沿MN折叠（M，N在AD、BC上），AD∥BC，C′，D′为C、D的对称点，C′N交AD于E．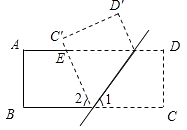 
（1）若∠1=62°，则∠2=
（2）试判断△EMN的形状，并说明理由．
【答案】
（1）56°
（2）解：△EMN为等腰三角形；理由如下：
由折叠的性质知：∠1=∠MNE，
又AD∥BC，
∴∠1=∠EMN，
∴∠MNE=∠EMN，
∴EN=EM，
即△EMN为等腰三角形．
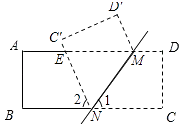
【解析】解：（1）如图所示：由折叠的性质得：∠MNE=∠1=62°， ∴∠2=180°﹣2×62°=56°；
所以答案是：56°；
【考点精析】通过灵活运用矩形的性质和翻折变换（折叠问题），掌握矩形的四个角都是直角，矩形的对角线相等；折叠是一种对称变换，它属于轴对称，对称轴是对应点的连线的垂直平分线，折叠前后图形的形状和大小不变，位置变化，对应边和角相等即可以解答此题．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
