题目内容
【题目】如图,已知直线y=﹣x+4与两坐标轴分别相交于点A,B两点,点C是线段AB上任意一点,过C分别作CD⊥x轴于点D,CE⊥y轴于点E.双曲线 ![]() 与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且
与CD,CE分别交于点P,Q两点,若四边形ODCE为正方形,且 ![]() ,则k的值是( )
,则k的值是( )
A.4
B.2
C.![]()
D.![]()
【答案】B
【解析】解:四边形ODCE为正方形,则OC是第一象限的角平分线,则解析式是y=x,
根据题意得: ![]() ,
,
解得: ![]() ,
,
则C的坐标是(2,2),
设Q的坐标是(2,a),
则DQ=EP=a,PC=CQ=2﹣a,
正方形ODCE的面积是:4,
S△ODQ= ![]() ×2a=a,同理S△OPE=a,S△CPQ=
×2a=a,同理S△OPE=a,S△CPQ= ![]() (2﹣a)2 ,
(2﹣a)2 ,
则4﹣a﹣a﹣ ![]() (2﹣a)2=
(2﹣a)2= ![]() ,
,
解得:a=1或﹣1(舍去),
则Q的坐标是(2,1),
把(2,1)代入 ![]() 得:k=2.
得:k=2.
故选B.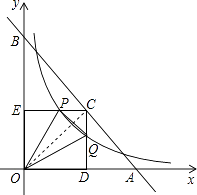
【考点精析】关于本题考查的反比例函数的概念和反比例函数的图象,需要了解形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点才能得出正确答案.

练习册系列答案
相关题目