题目内容
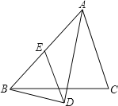
【题目】在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过D作DE∥AC,交AB于E,若BD=7,AD=24,求线段DE的长.
【答案】12.5
【解析】
利用AD平分得到∠BAD=∠CAD,再由DEAC证出∠ADE=∠CAD,得到AE=DE;由BD⊥AD得到△ABD是直角三角形,利用其它两个锐角互余求得BE=DE,从而得到DE=AE=BE,利用勾股定理求得AB即可得到DE的长度.
解:∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵DE∥AC,
∴∠CAD=∠ADE,
∴∠BAD=∠ADE,
∴AE=DE,
∵AD⊥DB,
∴∠ADB=90°,
∴∠EAD+∠ABD=90°,∠ADE+∠BDE=∠ADB=90°,
∴∠ABD=∠BDE,
∴DE=BE,
∵在Rt△ABD中,∠ADB=90°
∴AB=AD+BD,∴AB=25
∴DE=BE=AE=![]() AB=12.5
AB=12.5

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据求出表中a,b,c的值;
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | b |
乙 | a | 8 | 2.2 |
丙 | 6 | c | 3 |
(2)根据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定,用列举法求甲、乙相邻出场的概率.