题目内容
一辆快车从甲地驶往乙地,一辆慢车从乙地驶往甲地,两车同时出发,匀速行驶设行驶的时间为x(时),两车之间的距离为y(千米),图中的折线表示从两车出发至快车到达乙地过程中y与x之间的函数关系;

(1)根据图中信息,说明图中点(2,0)的实际意义;
(2)求图中线段AB所在直线的函数解析式和甲乙两地之间的距离;
(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;

(1)根据图中信息,说明图中点(2,0)的实际意义;
(2)求图中线段AB所在直线的函数解析式和甲乙两地之间的距离;
(3)已知两车相遇时快车比慢车多行驶40千米,若快车从甲地到达乙地所需时间为t时,求t的值;
(1)快车与慢车2小时相遇;
(2)AB:y=-140x+280,甲乙两地相差280千米;
(3)t=3.5
(2)AB:y=-140x+280,甲乙两地相差280千米;
(3)t=3.5
试题分析:(1)仔细分析题意结合图形特征即可作出判断;
(2)设图中线段AB所在直线的函数解析式为
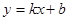 ,根据图象过点(1.5,70),(2,0)即可根据待定系数法求得函数解析式,再把
,根据图象过点(1.5,70),(2,0)即可根据待定系数法求得函数解析式,再把 代入即可求得甲乙两地之间的距离;
代入即可求得甲乙两地之间的距离;(3)先根据两车相遇时快车比慢车多行驶40千米求得快车的速度,再根据路程、速度、时间的关系即可求得结果.
(1)由题意得点(2,0)表示快车与慢车2小时相遇;
(2)设图中线段AB所在直线的函数解析式为
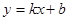
∵图象过点(1.5,70),(2,0)
∴
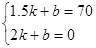 ,解得
,解得
∴线段AB所在直线的函数解析式为
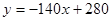
当
 时,
时,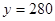
∴甲乙两地之间的距离为280千米;
(3)由题意得快车的速度为160÷2=80千米/时,则
 .
.点评:函数的应用是初中数学的重点和难点,在中考中极为常见,一般以压轴题形式出现,难度较大.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的图象与反比例函数
的图象与反比例函数 的图象交于点A(1,m),与x轴交于点
的图象交于点A(1,m),与x轴交于点 ,过点A作
,过点A作 轴于点
轴于点 .
.
 的坐标.
的坐标. .一次函数
.一次函数 的图象经过点B、C,反比例函数
的图象经过点B、C,反比例函数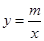 的图象经过点B.
的图象经过点B.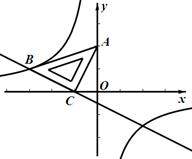
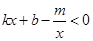 的解集;
的解集;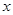 轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
轴上找一点M,使得AM+BM的值最小,并求出点M的坐标和AM+BM的最小值.
 经过
经过 ,
, 两点,求此一次函数的解析式;
两点,求此一次函数的解析式; 与坐标轴分别交于
与坐标轴分别交于 两点,动点
两点,动点 同时从
同时从 点出发,同时到达
点出发,同时到达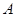 点,运动停止.点
点,运动停止.点 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点 沿路线
沿路线 →
→
 秒,
秒, 的面积为
的面积为 ,求出
,求出 时,求出点
时,求出点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点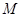 的坐标.
的坐标. 米,某天小敏从家里出发骑自行车上学,开始她以每分钟
米,某天小敏从家里出发骑自行车上学,开始她以每分钟 米的速度匀速行驶了
米的速度匀速行驶了 米,遇到交通堵塞,耽搁了
米,遇到交通堵塞,耽搁了 分钟,然后以每分钟
分钟,然后以每分钟 米的速度匀速前进一直到学校
米的速度匀速前进一直到学校 ,你认为小敏离家的距离
,你认为小敏离家的距离 与时间
与时间 之间的函数图象大致是( )
之间的函数图象大致是( )
 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 ,且
,且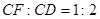 .设矩形
.设矩形 重叠部分的面积为
重叠部分的面积为 .
.
 、
、 的坐标;
的坐标; 值由小到大变化时,求
值由小到大变化时,求 ,使
,使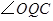 等于
等于 ,请直接写出
,请直接写出