题目内容
如图,在平面直角坐标系中,直线 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 轴上方作矩形
轴上方作矩形 ,且
,且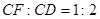 .设矩形
.设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.

(1)求点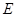 、
、 的坐标;
的坐标;
(2)当 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式;
(3)若在直线 上存在点
上存在点 ,使
,使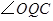 等于
等于 ,请直接写出
,请直接写出 的取值范围.
的取值范围.
 分别交
分别交 轴、
轴、 轴于
轴于 两点.点
两点.点 、
、 ,以
,以 为一边在
为一边在 轴上方作矩形
轴上方作矩形 ,且
,且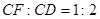 .设矩形
.设矩形 与
与 重叠部分的面积为
重叠部分的面积为 .
.
(1)求点
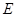 、
、 的坐标;
的坐标;(2)当
 值由小到大变化时,求
值由小到大变化时,求 与
与 的函数关系式;
的函数关系式;(3)若在直线
 上存在点
上存在点 ,使
,使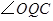 等于
等于 ,请直接写出
,请直接写出 的取值范围.
的取值范围.(1)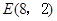 ,
,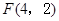 .(2)当0<b≤2时,
.(2)当0<b≤2时,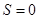 当2<b≤4时,
当2<b≤4时,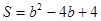
当4<b≤6时,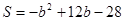 ④当b>6时,
④当b>6时,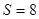 .(3)
.(3)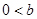 ≤
≤
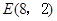 ,
,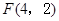 .(2)当0<b≤2时,
.(2)当0<b≤2时,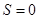 当2<b≤4时,
当2<b≤4时,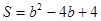
当4<b≤6时,
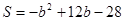 ④当b>6时,
④当b>6时,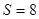 .(3)
.(3)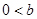 ≤
≤
试题分析:∵
 ,
, ,∴
,∴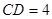 ,
,∵矩形
 中,
中,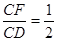 ,∴
,∴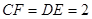 ,
,∵点
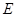 、
、 在第一象限,∴
在第一象限,∴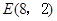 ,
,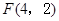 .
.由题意,可知
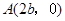 ,
,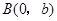 ,在Rt△ABO中,tan∠BAO=
,在Rt△ABO中,tan∠BAO=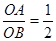 ,
,①当0<b≤2时,如图1,
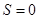 .
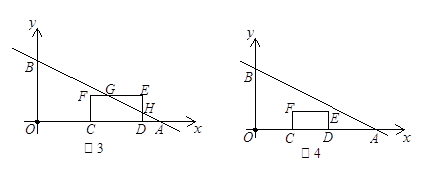
.②当2<b≤4时,如图2,设
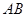 交
交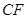 于
于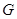 ,
,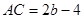 ,
,在Rt△AGC中,∵tan∠BAO=
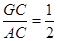 ,∴
,∴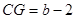 .
.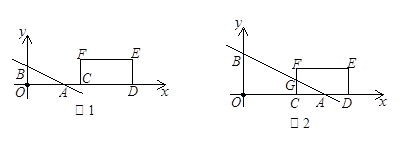
∴
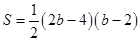 ,即
,即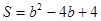 ,
,当4<b≤6时,如图3,设
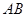 交
交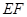 于
于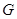 ,交
,交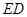 于
于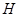 ,
,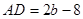 ,
,在Rt△ADH中,∵tan∠BAO=
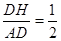 ,∴
,∴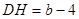 ,
,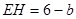 ,
,在矩形
 中,∵CD∥EF,∴∠EGH=∠BAO,
中,∵CD∥EF,∴∠EGH=∠BAO,在Rt△EGH中,∵tan∠EGH=
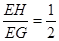 ,∴
,∴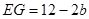 ,
,∴
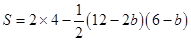 ,即
,即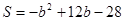 ,
,④当b>6时,如图4,
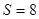 .
.点评:本题难度较大,主要考查学生对一次函数和动点问题综合运用解决几何图形问题的能力。为中考常见题型,学生要牢固掌握解题技巧。

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目


 ,
, ,求x和y的值.
,求x和y的值. ,
, )的直线解析式 .
)的直线解析式 .