题目内容
直线 与坐标轴分别交于
与坐标轴分别交于 两点,动点
两点,动点 同时从
同时从 点出发,同时到达
点出发,同时到达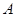 点,运动停止.点
点,运动停止.点 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点 沿路线
沿路线 →
→ →
→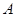 运动.
运动.

(1)直接写出 两点的坐标;
两点的坐标;
(2)设点 的运动时间为
的运动时间为 秒,
秒, 的面积为
的面积为 ,求出
,求出 与
与 之间的函数关系式;
之间的函数关系式;
(3)当 时,求出点
时,求出点 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点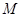 的坐标.
的坐标.
 与坐标轴分别交于
与坐标轴分别交于 两点,动点
两点,动点 同时从
同时从 点出发,同时到达
点出发,同时到达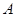 点,运动停止.点
点,运动停止.点 沿线段
沿线段 运动,速度为每秒1个单位长度,点
运动,速度为每秒1个单位长度,点 沿路线
沿路线 →
→ →
→ 运动.
运动.
(1)直接写出
 两点的坐标;
两点的坐标;(2)设点
 的运动时间为
的运动时间为 秒,
秒, 的面积为
的面积为 ,求出
,求出 与
与 之间的函数关系式;
之间的函数关系式;(3)当
 时,求出点
时,求出点 的坐标,并直接写出以点
的坐标,并直接写出以点 为顶点的平行四边形的第四个顶点
为顶点的平行四边形的第四个顶点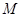 的坐标.
的坐标.(1)A(8,0)B(0,6);(2)当0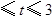 时,
时,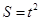 ,当
,当 时,
时,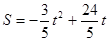 ;
;
(3)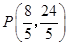 ,M1
,M1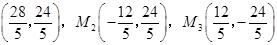
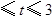 时,
时,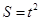 ,当
,当 时,
时,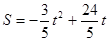 ;
;(3)
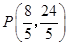 ,M1
,M1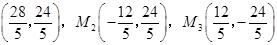
试题分析:(1)分别把
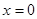 、
、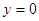 代入
代入 即可求得结果;
即可求得结果;(2)先根据勾股定理求得AB的长,根据点
 由
由 到
到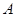 的时间可求得点
的时间可求得点 的速度,再分当
的速度,再分当 在线段
在线段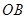 上运动(或0
上运动(或0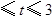 )时,当
)时,当 在线段
在线段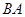 上运动(或
上运动(或 )时,两种情况,根据三角形的面积公式求解即可;
)时,两种情况,根据三角形的面积公式求解即可;(3)把
 代入(2)中的函数关系式即可求得点
代入(2)中的函数关系式即可求得点 的坐标,再根据平行四边形的性质求解即可.
的坐标,再根据平行四边形的性质求解即可.(1)A(8,0)B(0,6);
(2)
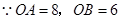
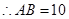
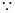 点
点 由
由 到
到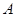 的时间是
的时间是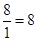 (秒)
(秒)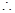 点
点 的速度是
的速度是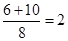 (单位/秒)
(单位/秒)当
 在线段
在线段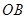 上运动(或0
上运动(或0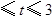 )时,
)时,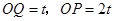 ,
,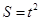
当
 在线段
在线段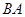 上运动(或
上运动(或 )时,
)时,
作
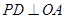 于点
于点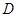 ,由
,由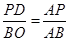 ,得
,得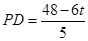 ,
,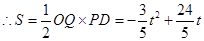 ;
;(3)
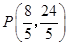 ,M1
,M1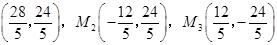
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目



 相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF.
相交于点D(-4,1)、C(1,m),并分别与坐标轴交于A、B两点,过点C作直线MN⊥x轴于F点,连接BF.

 (k≠0)的图象的大致位置是( )
(k≠0)的图象的大致位置是( )
 ,
, ,求x和y的值.
,求x和y的值.